DIF Statistical Inference and Detection without Knowing Anchoring Items

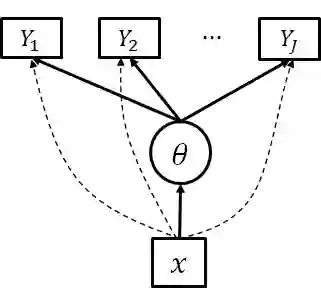
Establishing the invariance property of an instrument (e.g., a questionnaire or test) is a key step for establishing its measurement validity. Measurement invariance is typically assessed by differential item functioning (DIF) analysis, i.e., detecting DIF items whose response distribution depends not only on the latent trait measured by the instrument but also the group membership. DIF analysis is confounded by the group difference in the latent trait distributions. Many DIF analyses require to know several anchor items that are DIF-free and then draw inference on whether each of the rest is a DIF item, where the anchor items are used to calibrate the latent trait distributions. In this paper, we propose a new method for DIF analysis under a multiple indicators and multiple causes (MIMIC) model for DIF. This method adopts a minimal L1 norm condition for identifying the latent trait distributions. It can not only accurately estimate the DIF effects of individual items without requiring prior knowledge about an anchor set, but also draw valid statistical inference, which yields accurate detection of DIF items. The inference results further allow us to control the type-I error for DIF detection. We conduct simulation studies to evaluate the performance of the proposed method and compare it with the anchor-set-based likelihood ratio test approach and the LASSO approach. The proposed method is further applied to analyzing the three personality scales of Eysenck personality questionnaire - revised (EPQ-R).