On the Optimal Combination of Cross-Entropy and Soft Dice Losses for Lesion Segmentation with Out-of-Distribution Robustness

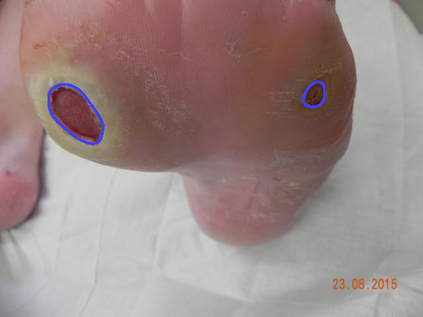
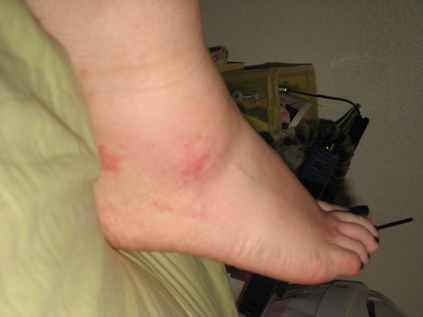
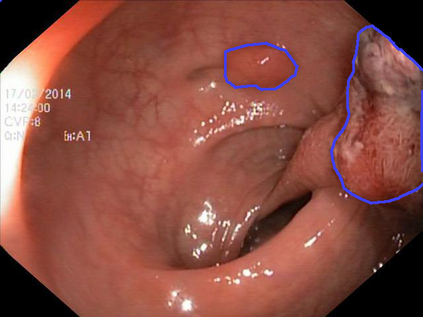
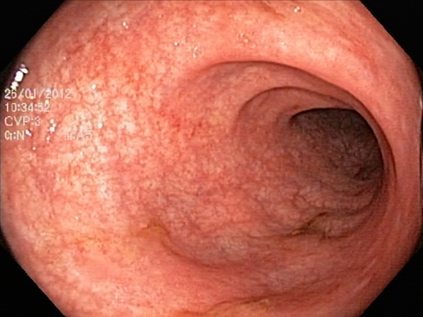
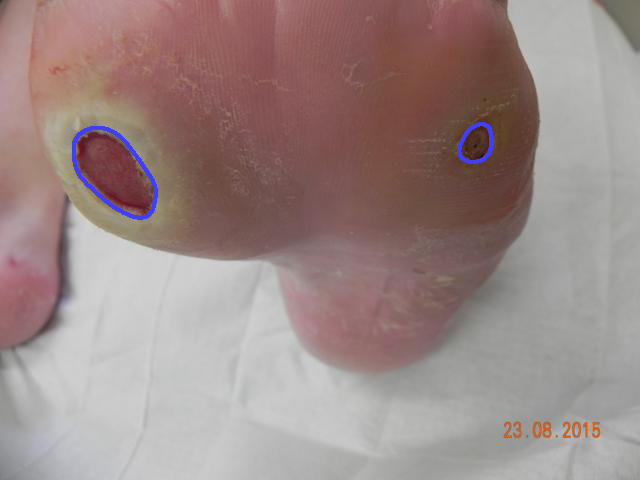
We study the impact of different loss functions on lesion segmentation from medical images. Although the Cross-Entropy (CE) loss is the most popular option when dealing with natural images, for biomedical image segmentation the soft Dice loss is often preferred due to its ability to handle imbalanced scenarios. On the other hand, the combination of both functions has also been successfully applied in this kind of tasks. A much less studied problem is the generalization ability of all these losses in the presence of Out-of-Distribution (OoD) data. This refers to samples appearing in test time that are drawn from a different distribution than training images. In our case, we train our models on images that always contain lesions, but in test time we also have lesion-free samples. We analyze the impact of the minimization of different loss functions on in-distribution performance, but also its ability to generalize to OoD data, via comprehensive experiments on polyp segmentation from endoscopic images and ulcer segmentation from diabetic feet images. Our findings are surprising: CE-Dice loss combinations that excel in segmenting in-distribution images have a poor performance when dealing with OoD data, which leads us to recommend the adoption of the CE loss for this kind of problems, due to its robustness and ability to generalize to OoD samples. Code associated to our experiments can be found at \url{https://github.com/agaldran/lesion_losses_ood} .