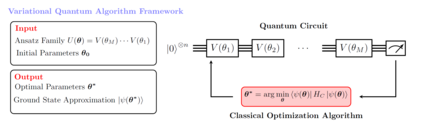
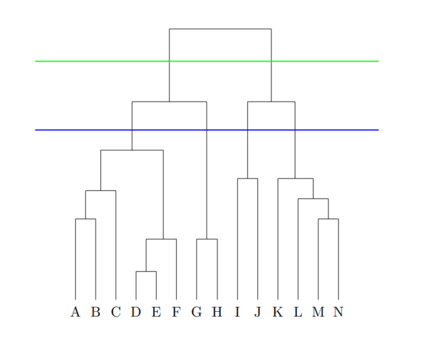
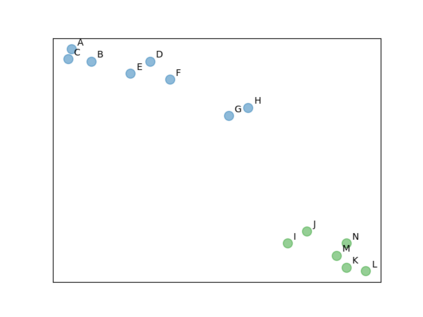
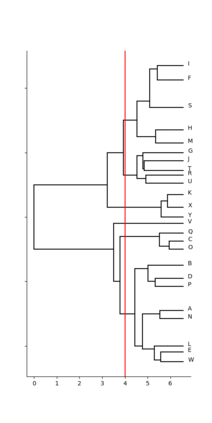
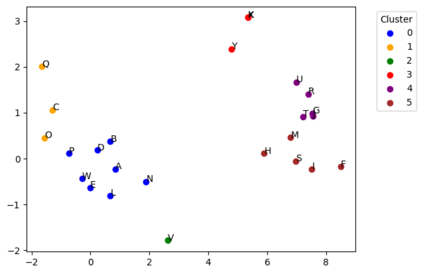
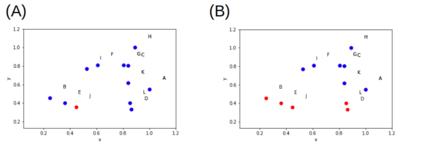
Current quantum hardware prohibits any direct use of large classical datasets. Coresets allow for a succinct description of these large datasets and their solution in a computational task is competitive with the solution on the original dataset. The method of combining coresets with small quantum computers to solve a given task that requires a large number of data points was first introduced by Harrow [arXiv:2004.00026]. In this paper, we apply the coreset method in three different well-studied classical machine learning problems, namely Divisive Clustering, 3-means Clustering, and Gaussian Mixture Model Clustering. We provide a Hamiltonian formulation of the aforementioned problems for which the number of qubits scales linearly with the size of the coreset. Then, we evaluate how the variational quantum eigensolver (VQE) performs on these problems and demonstrate the practical efficiency of coresets when used along with a small quantum computer. We perform noiseless simulations on instances of sizes up to 25 qubits on CUDA Quantum and show that our approach provides comparable performance to classical solvers.
翻译:暂无翻译