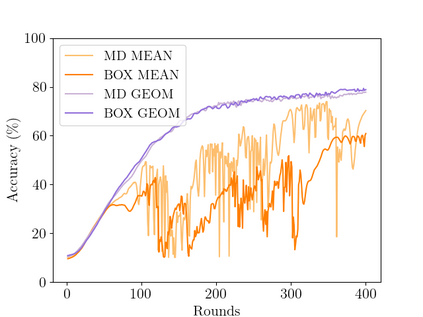
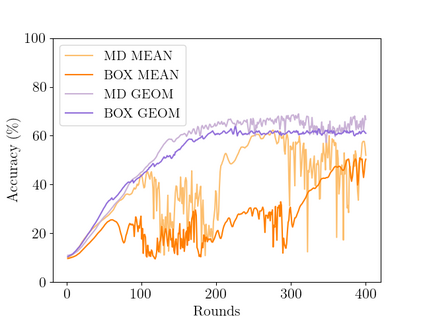
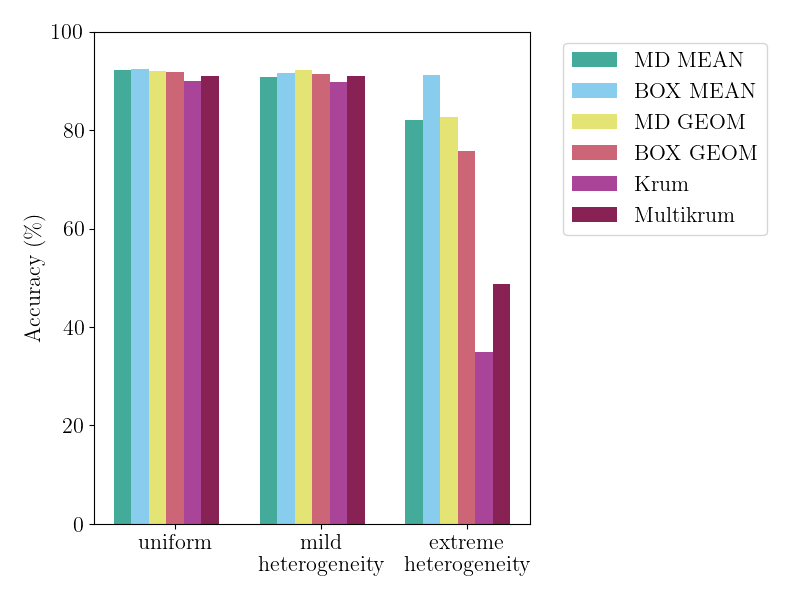
In Byzantine collaborative learning, $n$ clients in a peer-to-peer network collectively learn a model without sharing their data by exchanging and aggregating stochastic gradient estimates. Byzantine clients can prevent others from collecting identical sets of gradient estimates. The aggregation step thus needs to be combined with an efficient (approximate) agreement subroutine to ensure convergence of the training process. In this work, we study the geometric median aggregation rule for Byzantine collaborative learning. We show that known approaches do not provide theoretical guarantees on convergence or gradient quality in the agreement subroutine. To satisfy these theoretical guarantees, we present a hyperbox algorithm for geometric median aggregation. We practically evaluate our algorithm in both centralized and decentralized settings under Byzantine attacks on non-i.i.d. data. We show that our geometric median-based approaches can tolerate sign-flip attacks better than known mean-based approaches from the literature.
翻译:暂无翻译