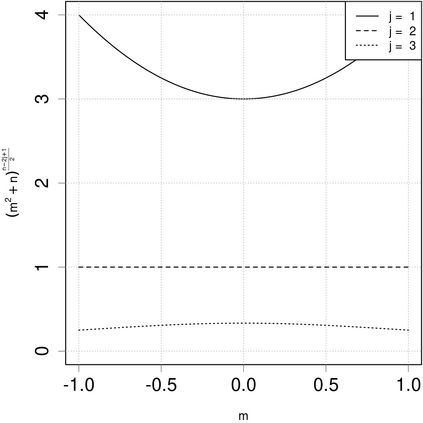
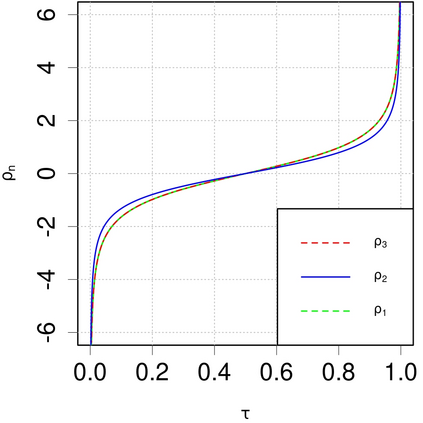
This paper introduces inter-order formulas for partial and complete moments of a Student $t$ distribution with $n$ degrees of freedom. We show how the partial moment of order $n - j$ about any real value $m$ can be expressed in terms of the partial moment of order $j - 1$ for $j$ in $\{1,\dots, n \}$. Closed form expressions for the complete moments are also established. We then focus on $L_p$-quantiles, which represent a class of generalized quantiles defined through an asymmetric $p$-power loss function. Based on the results obtained, we also show that for a Student $t$ distribution the $L_{n-j+1}$-quantile and the $L_j$-quantile coincide at any confidence level $\tau$ in $(0, 1)$.
翻译:本文引入了部分和完整时间分配学生用美元分配的部分和完整时间的顺序间公式, 以美元为单位的自由度为单位。 我们展示了部分时间的顺序(n- j$, 任何实际价值为百万美元)如何以部分时间的顺序($- 1美元, 美元, 美元, 美元, 美元, 美元, 美元, 美元, 美元, 美元, 美元, 美元, 美元) 表示完整时间的封闭形式表达方式 。 然后我们关注 $_ p$- quantiles, 代表一种通过不对称的美元损失功能定义的通用量化的类别 。 根据所获得的结果, 我们还显示,对于学生来说, 美元, 美元, 美元, 美元, 美元, 美元, 美元, 美元, 美元, 美元, 美元, 美元, 美元。 美元。