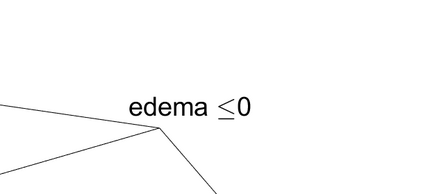
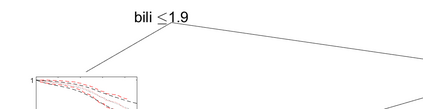
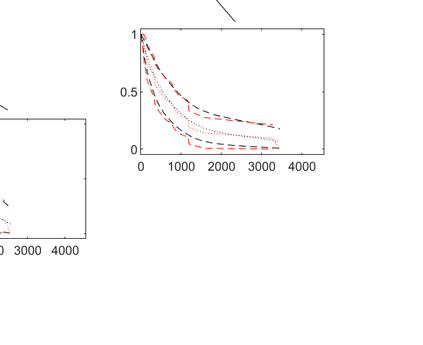
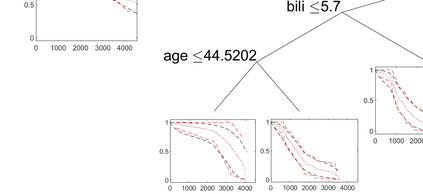
Survival models are used to analyze time-to-event data in a variety of disciplines. Proportional hazard models provide interpretable parameter estimates, but proportional hazards assumptions are not always appropriate. Non-parametric models are more flexible but often lack a clear inferential framework. We propose a Bayesian tree partition model which is both flexible and inferential. Inference is obtained through the posterior tree structure and flexibility is preserved by modeling the the hazard function in each partition using a latent exponentiated Gaussian process. An efficient reversible jump Markov chain Monte Carlo algorithm is accomplished by marginalizing the parameters in each partition element via a Laplace approximation. Consistency properties for the estimator are established. The method can be used to help determine subgroups as well as prognostic and/or predictive biomarkers in time-to-event data. The method is applied to a liver survival dataset and is compared with some existing methods on simulated data.
翻译:比例危害模型提供可解释的参数估计,但相称的危害假设并不总是适当的。非参数模型比较灵活,但往往缺乏明确的推论框架。我们提议了一种灵活和推断性的巴伊西亚树分隔模型。通过后树结构获得推论,通过利用潜在引力高斯进程模拟每个分区的危险函数,保持灵活性。高效的可逆跳跃马尔科夫链蒙特卡洛算法是通过拉比近差使每个分区要素的参数边缘化而实现的。确定了估测器的粘性特性。该方法可用于在时间到活动数据中确定分组以及预测和/或预测生物标记。该方法用于肝脏生存数据集,并与模拟数据的某些现有方法进行比较。