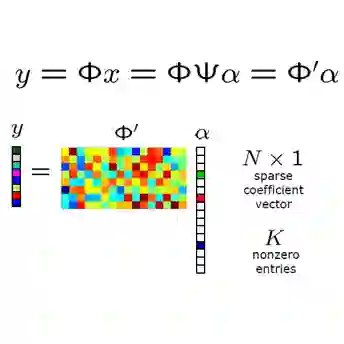
Separable multi-block convex optimization problem appears in many mathematical and engineering fields. In the first part of this paper, we propose an inertial proximal ADMM to solve a linearly constrained separable multi-block convex optimization problem, and we show that the proposed inertial proximal ADMM has global convergence under mild assumptions on the regularization matrices. Affine phase retrieval arises in holography, data separation and phaseless sampling, and it is also considered as a nonhomogeneous version of phase retrieval that has received considerable attention in recent years. Inspired by convex relaxation of vector sparsity and matrix rank in compressive sensing and by phase lifting in phase retrieval, in the second part of this paper, we introduce a compressive affine phase retrieval via lifting approach to connect affine phase retrieval with multi-block convex optimization, and then based on the proposed inertial proximal ADMM for multi-block convex optimization, we propose an algorithm to recover sparse real signals from their (noisy) affine quadratic measurements. Our numerical simulations show that the proposed algorithm has satisfactory performance for affine phase retrieval of sparse real signals.
翻译:在许多数学和工程学领域,都出现了多分解的多区锥形优化问题。在本文件第一部分,我们建议采用惯性准亚性ADMM,以解决线性受限制的可分解多区锥形优化问题,并表明拟议的惯性准亚性ADMM在正规化矩阵的轻度假设下具有全球趋同性。在全息学、数据分离和无阶段抽样中出现偏移阶段检索问题,并且它也被视为一种不相异的阶段检索版本,近年来受到相当重视。在压缩感中的矢量散变宽和矩阵级松散,以及在阶段检索中逐步提升的激励下,我们在本文第二部分,采用了一个通过提升方法将离子阶段的检索与多区锥形锥形优化联系起来的压缩形相片次检索,然后根据拟议的多区锥形锥形峰优化的惯性亚性ADMMMMM,我们提出一种算法,以从它们(不易碎裂)的四边测量中恢复零散真实信号。我们的数字模拟显示,拟议的真实的反向阶段恢复信号是令人满意的。