Application and Assessment of Divide-and-Conquer-based Heuristic Algorithms for some Integer Optimization Problems

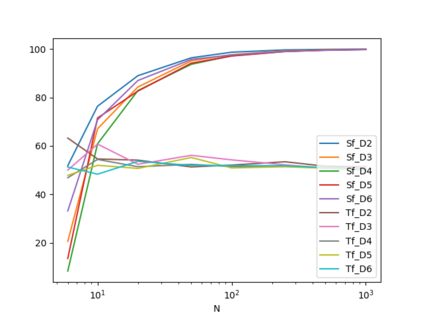
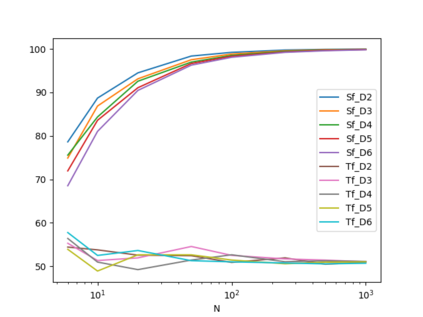
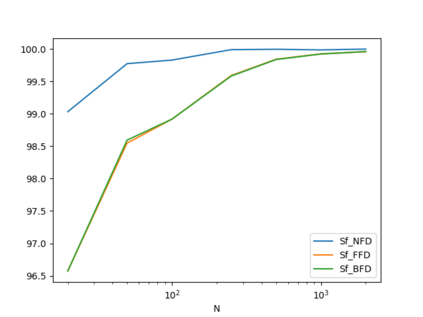
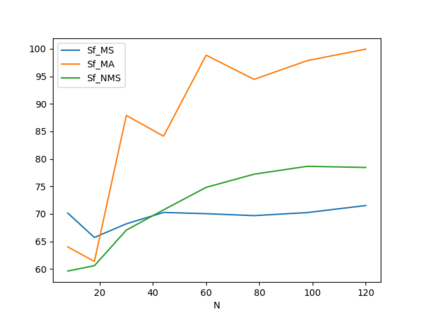
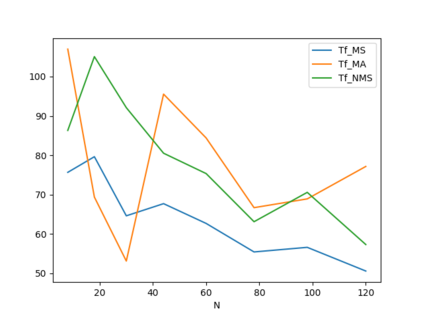
In this paper three heuristic algorithms using the Divide-and-Conquer paradigm are developed and assessed for three integer optimizations problems: Multidimensional Knapsack Problem (d-KP), Bin Packing Problem (BPP) and Travelling Salesman Problem (TSP). For each case, the algorithm is introduced, together with the design of numerical experiments, in order to empirically establish its performance from both points of view: its computational time and its numerical accuracy.