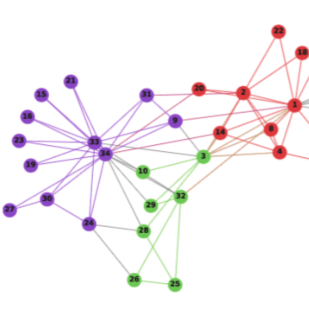
Researchers have designed many algorithms to measure the distances between graph nodes, such as average hitting times of random walks, cosine distances from DeepWalk, personalized PageRank, etc. Successful although these algorithms are, still they are either underperforming or too time-consuming to be applicable to huge graphs that we encounter daily in this big data era. To address these issues, here we propose a faster algorithm based on an improved version of random walks that can beat DeepWalk results with more than ten times acceleration. The reason for this significant acceleration is that we can derive an analytical formula to calculate the expected hitting times of this random walk quickly. There is only one parameter (the power expansion order) in our algorithm, and the results are robust with respect to its changes. Therefore, we can directly find the optimal solution without fine-tuning of model parameters. Our method can be widely used for fraud detection, targeted ads, recommendation systems, topic-sensitive search, etc.
翻译:研究人员设计了许多算法,以测量图形节点之间的距离,例如随机行走的平均点击时间、与深电站的焦距距离、个性化的PageRank等。 成功虽然这些算法是成功的, 但仍表现不佳或过于耗时, 无法适用于我们在这个大数据时代每天遇到的巨型图表。 为了解决这些问题, 我们在此建议一个基于改进版随机行走速度的快速算法, 可以以10倍以上的加速率击败深海行走结果。 如此显著加速的原因是我们可以得出一个分析公式, 以快速计算这种随机行走的预期点击时间。 我们的算法中只有一个参数( 权力扩展顺序), 其结果在变化方面是稳健的。 因此, 我们可以直接找到最佳的解决方案, 不微调模型参数。 我们的方法可以被广泛用于欺诈检测、 定向广告、 建议系统、 专题敏感搜索等 。