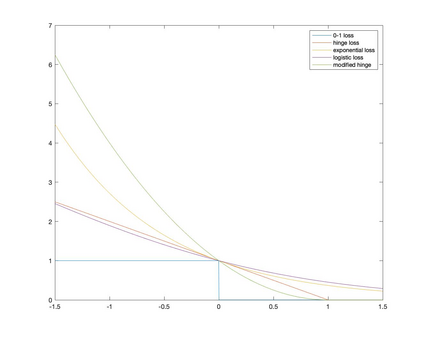
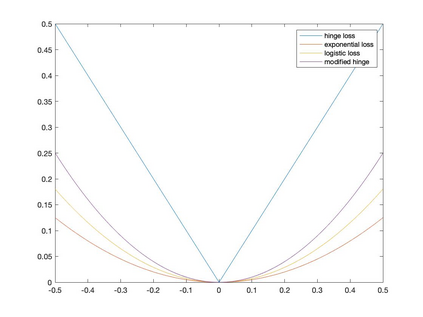
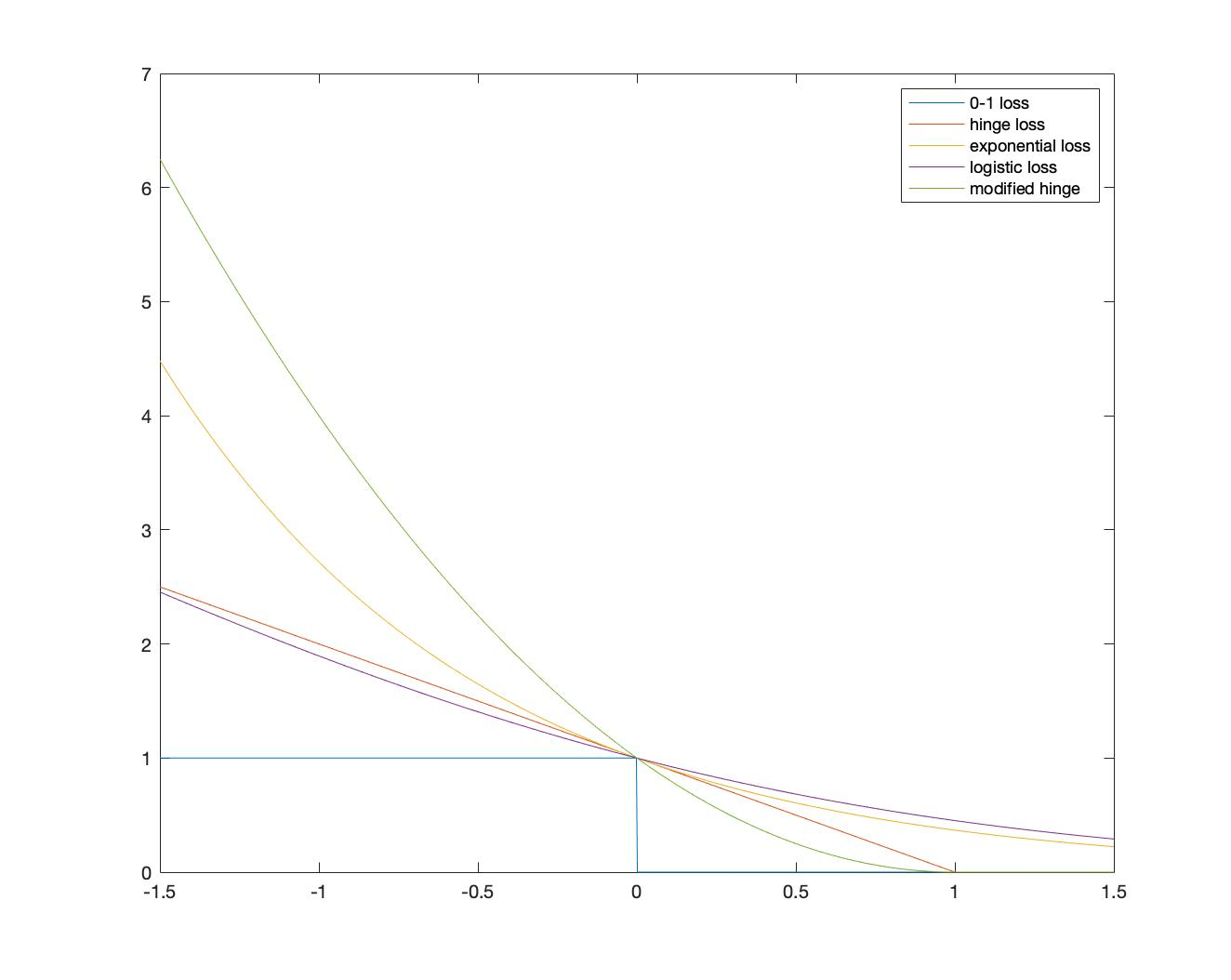
We study the rates of convergence from empirical surrogate risk minimizers to the Bayes optimal classifier. Specifically, we introduce the notion of \emph{consistency intensity} to characterize a surrogate loss function and exploit this notion to obtain the rate of convergence from an empirical surrogate risk minimizer to the Bayes optimal classifier, enabling fair comparisons of the excess risks of different surrogate risk minimizers. The main result of the paper has practical implications including (1) showing that hinge loss is superior to logistic and exponential loss in the sense that its empirical minimizer converges faster to the Bayes optimal classifier and (2) guiding to modify surrogate loss functions to accelerate the convergence to the Bayes optimal classifier.
翻译:我们研究了从经验替代风险最小化器到贝耶斯最佳分类器的趋同率。具体地说,我们引入了代用损失功能特征概念,并利用这一概念从经验替代风险最小化器到贝耶斯最佳分类器取得经验替代风险最小化器的趋同率,以便对不同代用风险最小化器的过重风险进行公平比较。文件的主要结果具有实际影响,包括:(1) 表明临界损失优于物流和指数损失,因为其经验最小化器更快地与贝耶斯最佳分类器汇合,(2) 指导如何修改代用损失功能,加快与贝耶斯最佳分类器的趋同。