Splitted Levenberg-Marquardt Method for Large-Scale Sparse Problems

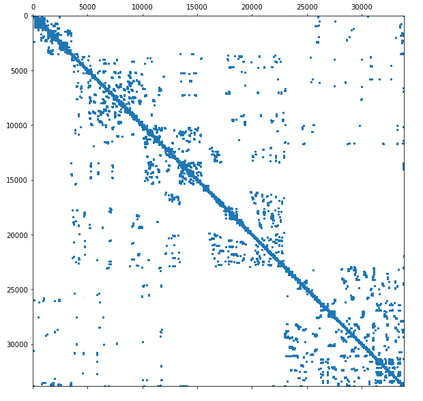
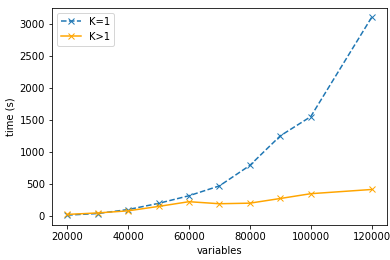
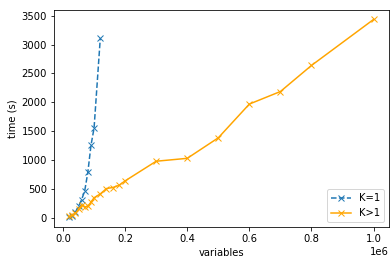
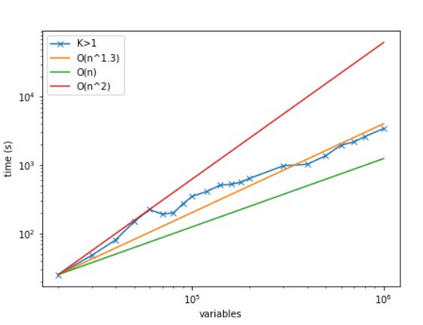
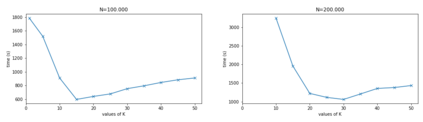
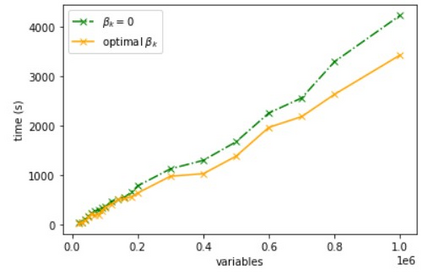
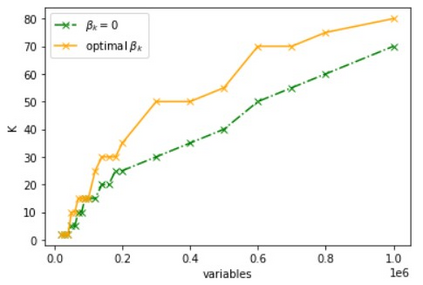
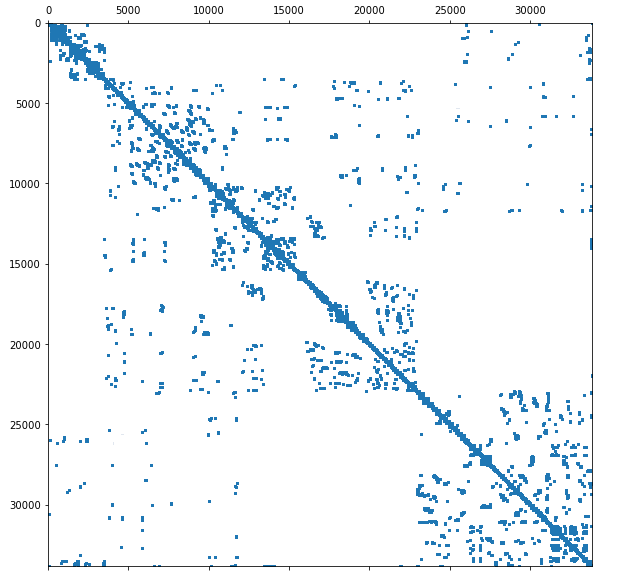
We consider large-scale nonlinear least squares problems with sparse residuals, each one of them depending on a small number of variables. A decoupling procedure which results in a splitting of the original problems into a sequence of independent problems of smaller sizes is proposed and analysed. The smaller size problems are modified in a way that offsets the error made by disregarding dependencies that allow us to split the original problem. The resulting method is a modification of the Levenberg-Marquardt method with smaller computational costs. Global convergence is proved as well as local linear convergence under suitable assumptions on sparsity. The method is tested on the network localization simulated problems with up to one million variables and its efficiency is demonstrated.