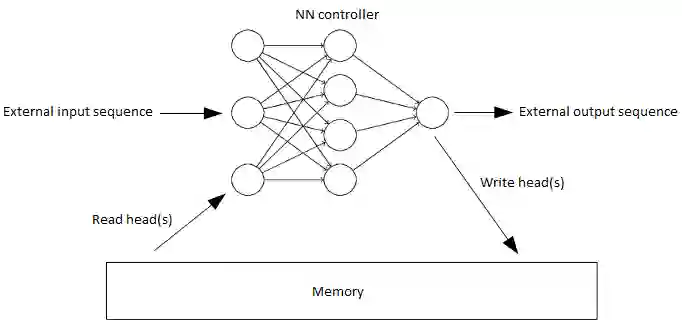
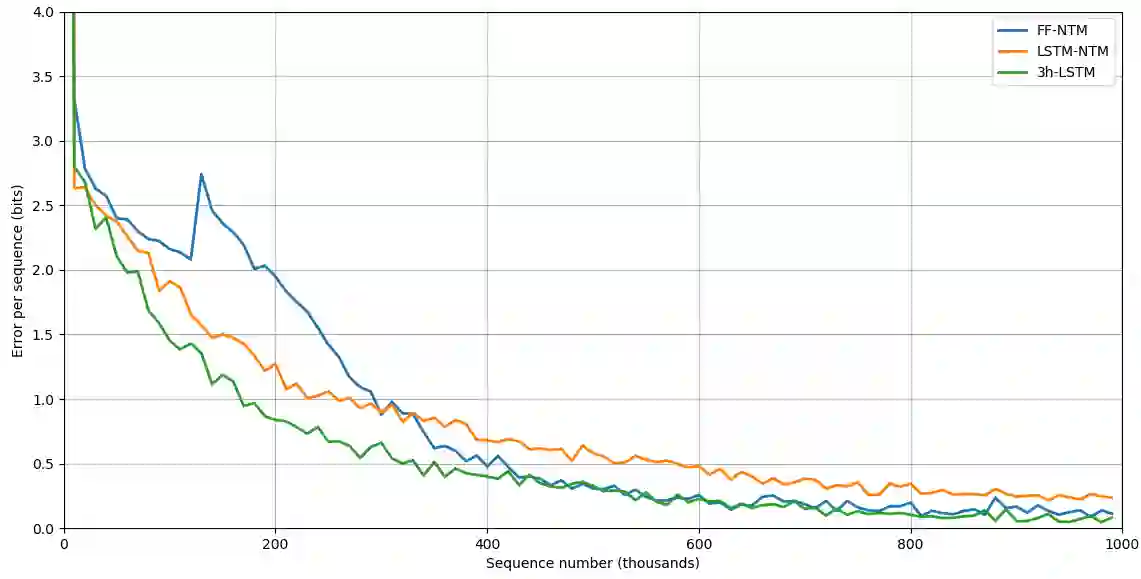
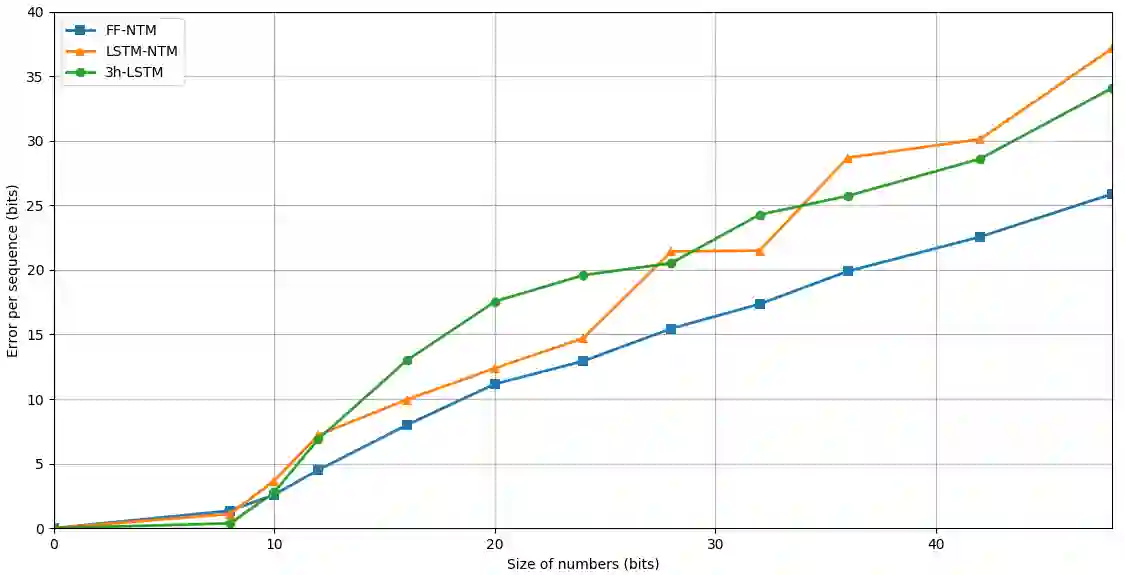
One of the main problems encountered so far with recurrent neural networks is that they struggle to retain long-time information dependencies in their recurrent connections. Neural Turing Machines (NTMs) attempt to mitigate this issue by providing the neural network with an external portion of memory, in which information can be stored and manipulated later on. The whole mechanism is differentiable end-to-end, allowing the network to learn how to utilise this long-term memory via stochastic gradient descent. This allows NTMs to infer simple algorithms directly from data sequences. Nonetheless, the model can be hard to train due to a large number of parameters and interacting components and little related work is present. In this work we use NTMs to learn and generalise two arithmetical tasks: binary addition and multiplication. These tasks are two fundamental algorithmic examples in computer science, and are a lot more challenging than the previously explored ones, with which we aim to shed some light on the real capabilities on this neural model.
翻译:神经神经网络(NTMs)试图通过向神经网络提供内存的外部部分来缓解这一问题,其中信息可以储存并随后加以操作。整个机制是不同的端对端,使网络能够学习如何通过随机梯度梯度下降来利用这一长期记忆。这使得NTMs能够直接从数据序列中推断简单的算法。然而,由于有大量参数和互动组件,而且几乎没有相关工作,模型可能很难培训。在这项工作中,我们利用NTMs学习和概括两种算术任务:二进制和乘法。这些任务是计算机科学的两个基本的算法实例,比以前所探讨的那些例子更具挑战性,我们打算用这些例子来说明这个神经模型的真正能力。