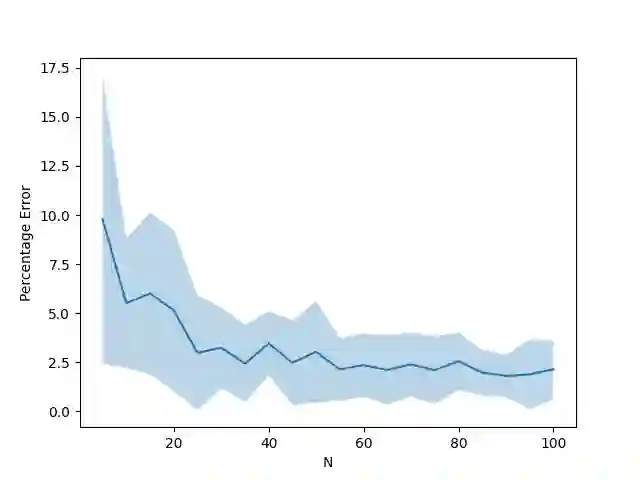
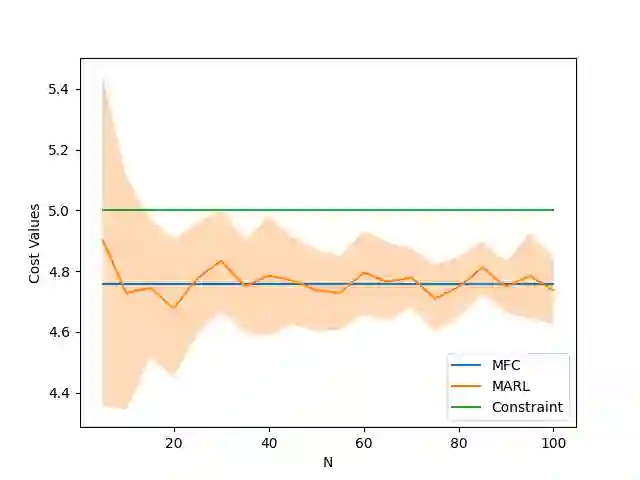
Mean-Field Control (MFC) has recently been proven to be a scalable tool to approximately solve large-scale multi-agent reinforcement learning (MARL) problems. However, these studies are typically limited to unconstrained cumulative reward maximization framework. In this paper, we show that one can use the MFC approach to approximate the MARL problem even in the presence of constraints. Specifically, we prove that, an $N$-agent constrained MARL problem, with state, and action spaces of each individual agents being of sizes $|\mathcal{X}|$, and $|\mathcal{U}|$ respectively, can be approximated by an associated constrained MFC problem with an error, $e\triangleq \mathcal{O}\left([\sqrt{|\mathcal{X}|}+\sqrt{|\mathcal{U}|}]/\sqrt{N}\right)$. In a special case where the reward, cost, and state transition functions are independent of the action distribution of the population, we prove that the error can be improved to $e=\mathcal{O}(\sqrt{|\mathcal{X}|}/\sqrt{N})$. Also, we provide a Natural Policy Gradient based algorithm and prove that it can solve the constrained MARL problem within an error of $\mathcal{O}(e)$ with a sample complexity of $\mathcal{O}(e^{-6})$.
翻译:常规战地控制(MFC)最近被证明是一个可推广的工具,可以大致解决大型多试剂强化学习(MARL)问题。然而,这些研究通常仅限于不受限制的累积奖励最大化框架。在本文中,我们表明,即使存在制约,也可以使用MFC方法来接近MARL问题。具体地说,我们证明,一个由美元代理公司限制的MARL问题,每个个体代理人的奖赏、成本和动作空间都分别大小为 $ mathal{X ⁇ }和 $ mathal{U_Cal_Cal_BAR_BAR_BAR_BAR_BAR_BAR_BAR_BAR_BAR_BAR_BAR_BAR_BAR_BAR_BAR_BAR_BAR_BAR_BAR_BAR_BAR_BAR_BAR_CFCFCFCFCFCFCFCFC $\ $\ $_BAR_BAR_BAR_BAR_BAR_BAR_BAR_BC_BAR_BAR_BAR_BAR_BAR_BAR_BAR_BAR_BAR_BAR_BAR_BAR_BAR_B_BAR_BAR_BAR__BAR_BAR________BAR_BAR___BAR_____BAR_BAR___BAR_BAR_BAR_________BAR_BAR_BAR_BAR_BAR_BAR______BAR_BAR_BAR_BAR_BAR_BAR_____________BAR__________B_______________________________BAR_____BAR_BAR_____BAR_______BAR_BAR_________________________B}