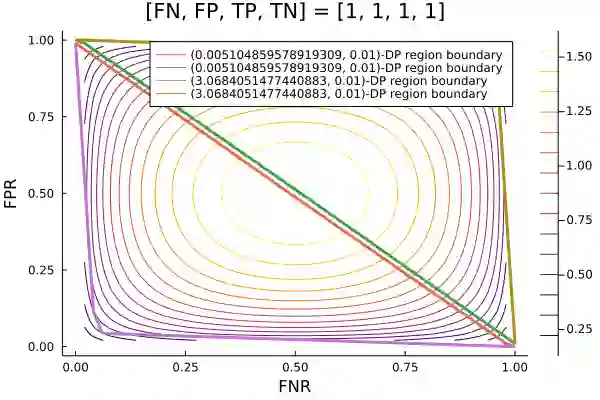
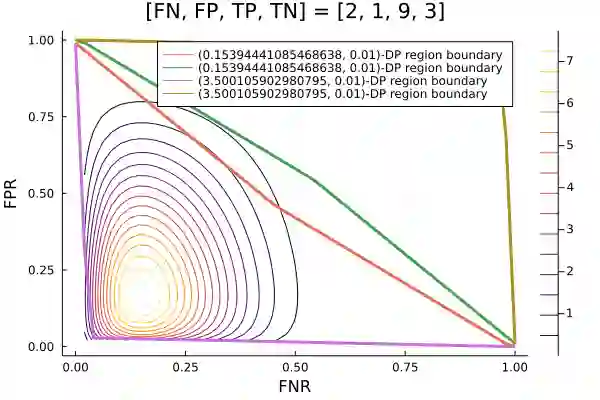
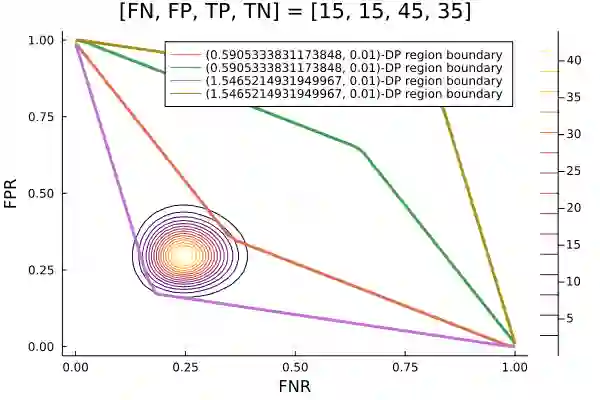
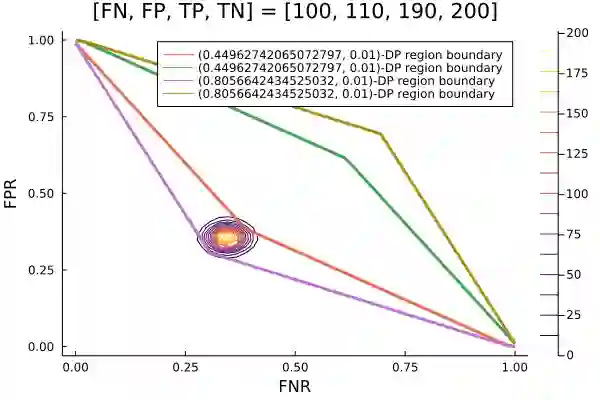
Algorithms such as Differentially Private SGD enable training machine learning models with formal privacy guarantees. However, there is a discrepancy between the protection that such algorithms guarantee in theory and the protection they afford in practice. An emerging strand of work empirically estimates the protection afforded by differentially private training as a confidence interval for the privacy budget $\varepsilon$ spent on training a model. Existing approaches derive confidence intervals for $\varepsilon$ from confidence intervals for the false positive and false negative rates of membership inference attacks. Unfortunately, obtaining narrow high-confidence intervals for $\epsilon$ using this method requires an impractically large sample size and training as many models as samples. We propose a novel Bayesian method that greatly reduces sample size, and adapt and validate a heuristic to draw more than one sample per trained model. Our Bayesian method exploits the hypothesis testing interpretation of differential privacy to obtain a posterior for $\varepsilon$ (not just a confidence interval) from the joint posterior of the false positive and false negative rates of membership inference attacks. For the same sample size and confidence, we derive confidence intervals for $\varepsilon$ around 40% narrower than prior work. The heuristic, which we adapt from label-only DP, can be used to further reduce the number of trained models needed to get enough samples by up to 2 orders of magnitude.
翻译:差异私人SGD等解算法使培训机器学习模式具有正式的隐私保障。然而,这种算法在理论上保障的保护与实际保护之间存在差异。正在出现的工作对不同私人培训作为隐私预算信任间隔提供的保护进行了实证估计,这是花在培训模型上花费的美元作为隐私预算信任间隔。现有方法从虚假正值和负值成员攻击的假正值和负值比信任间隔中得出美元的信任度间隔。不幸的是,使用这种方法获得对$\efslon的狭义高信任间隔需要不切实际的大样本规模和对与样本一样的众多模型进行培训。我们建议采用新颖的贝叶斯法方法,大大缩小样本规模,调整和校正理论,以便根据经过培训的模型绘制不止一个样本。我们的巴伊西亚方法利用对差异隐私权的假设测试,以便从假正值和负值成员攻击的假正值和负值攻击的假正值联合海报间隔。对于类似样本规模和假负值攻击的40美元攻击,我们需要用新的贝斯方法来降低我们之前的信心。我们所使用的标准,可以进一步修改。