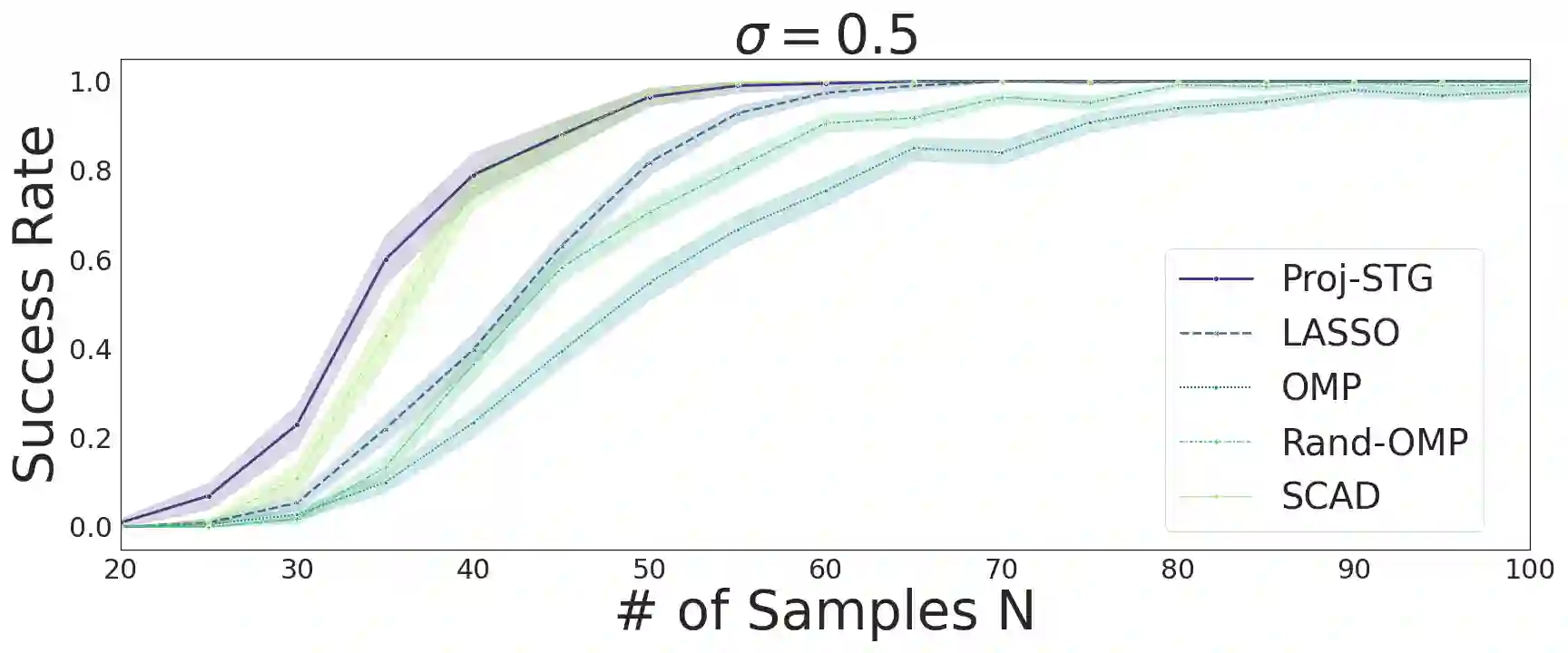
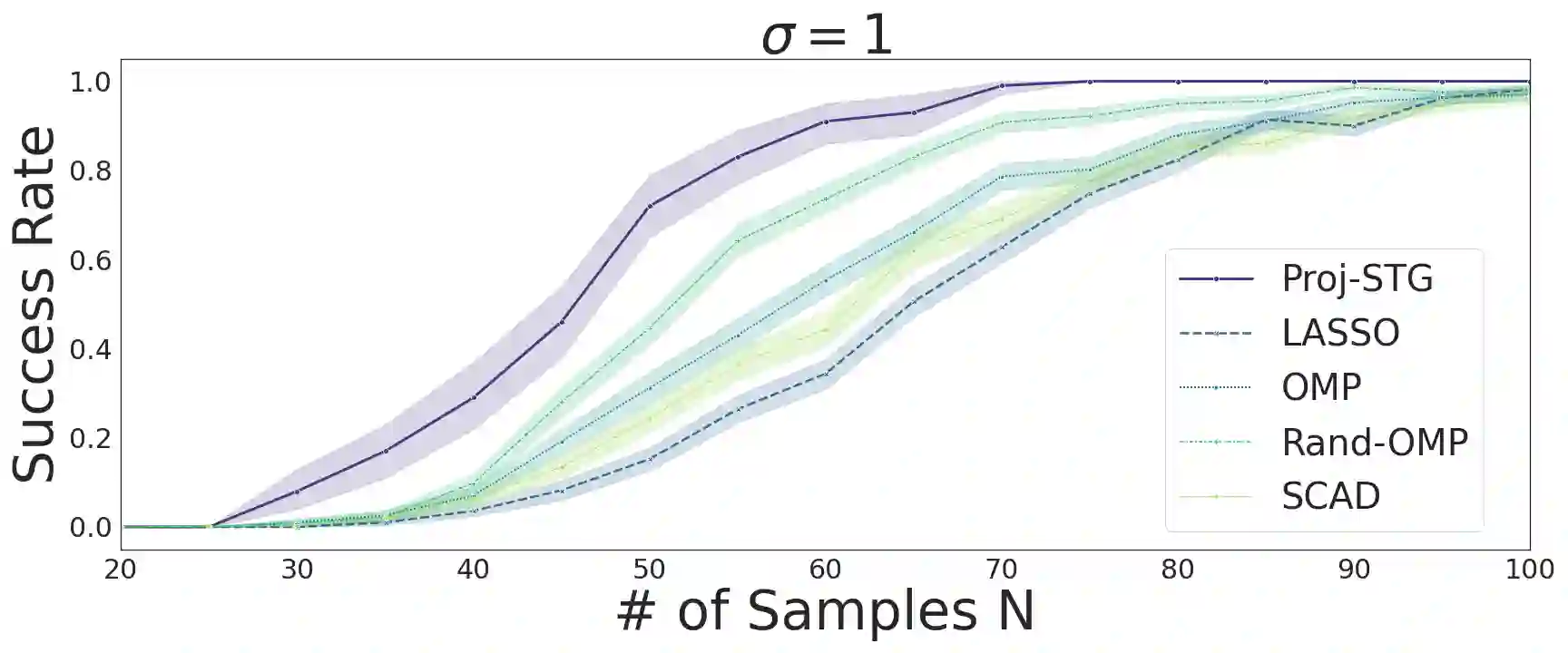
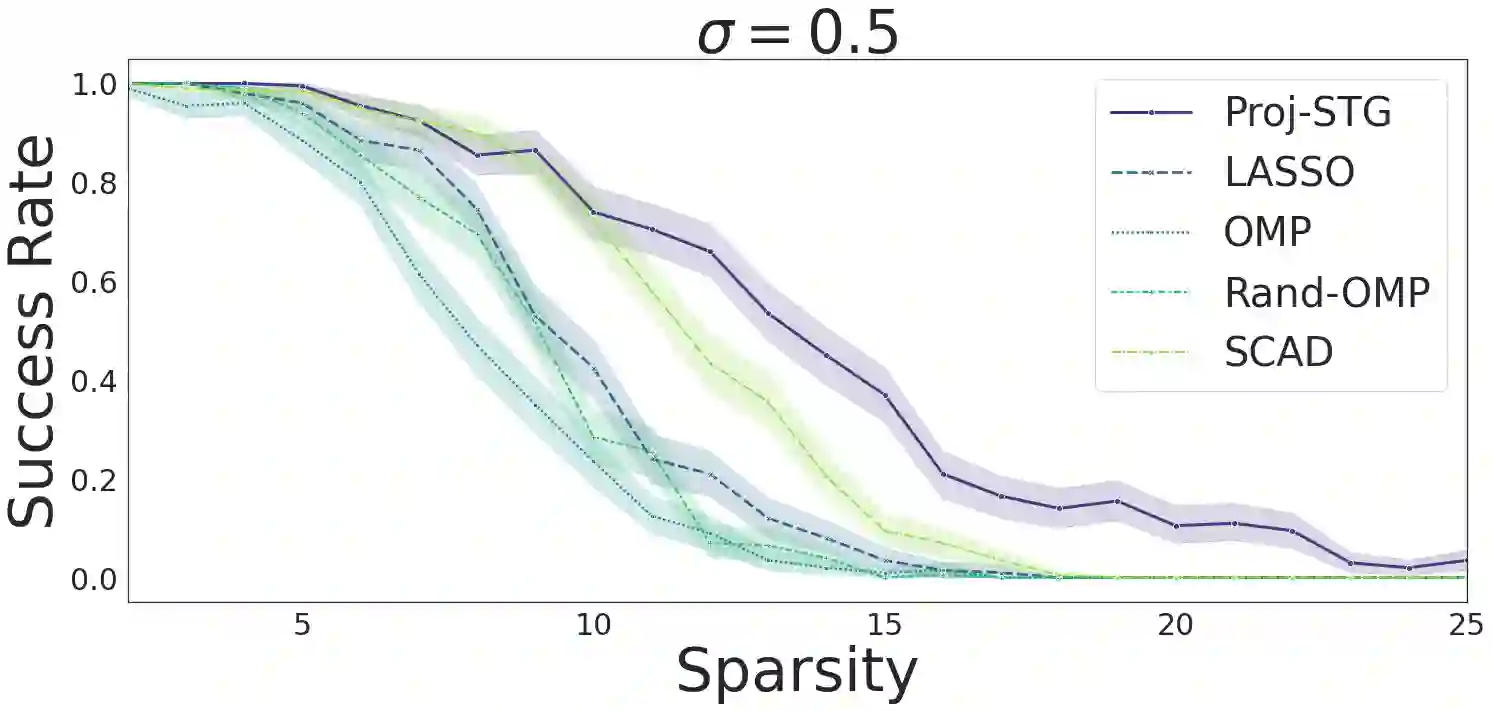
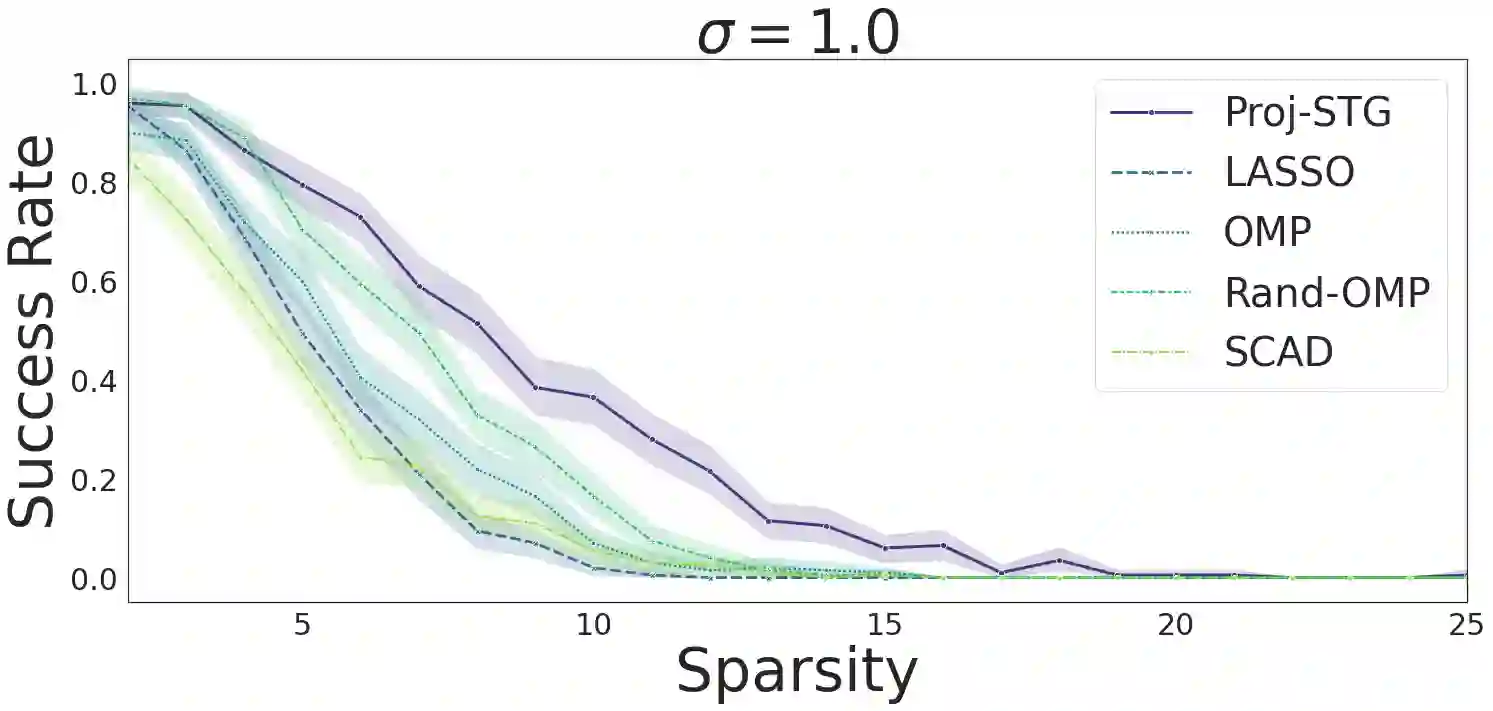
We analyze the problem of simultaneous support recovery and estimation of the coefficient vector ($\beta^*$) in a linear model with independent and identically distributed Normal errors. We apply the penalised least square estimator of $\beta^*$ based on non-linear penalties of stochastic gates (STG) [YLNK20] to estimate the coefficients. Considering Gaussian design matrices we show that under reasonable conditions on dimension and sparsity of $\beta^*$ the STG based estimator converges to the true data generating coefficient vector and also detects its support set with high probability. We propose a new projection based algorithm for the linear models setup to improve upon the existing STG estimator that was originally designed for general non-linear models. Our new procedure outperforms many classical estimators for sparse support recovery in synthetic data analysis.
翻译:我们用独立且分布相同的正常错误的线性模型分析同时支持回收和估计系数矢量( $\beta ⁇ $) 的问题。 我们使用基于非线性罚款的最小平方估计值$\beta ⁇ $[YLNK20] 来估计系数。 考虑到高斯设计矩阵, 我们显示,在维度和宽度的合理条件下, 以STG 为基础的估计值会与真正的数据生成系数矢量汇合, 并发现其支持性设定的概率很高。 我们建议基于线性模型设置的基于新算法的预测值, 以改进原为一般非线性模型设计的现有的STG 估计值。 我们的新程序在合成数据分析中, 将许多经典的测量值转化为稀少支持性恢复。