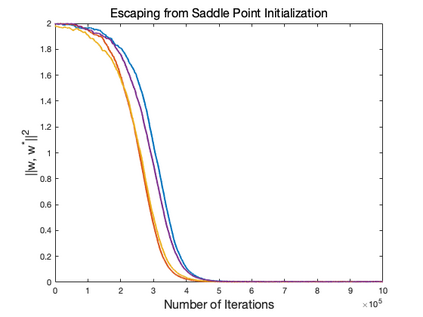
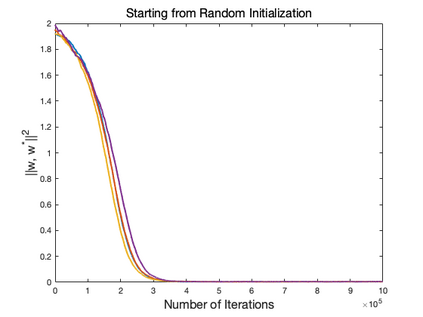
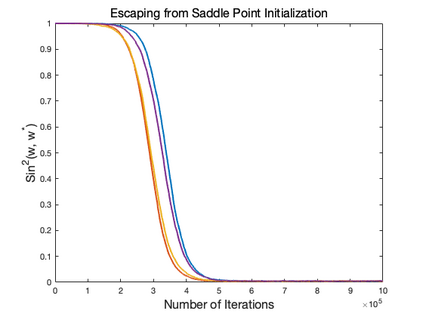
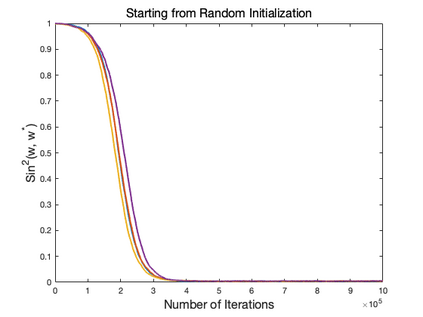
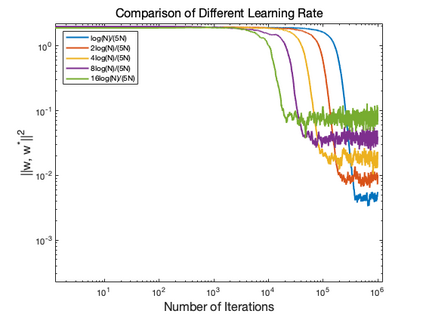
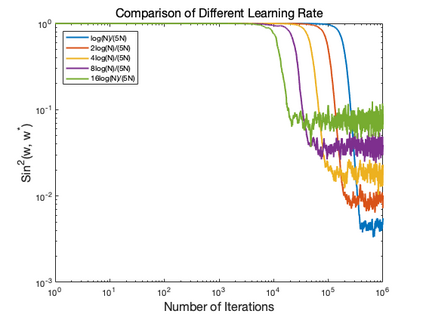
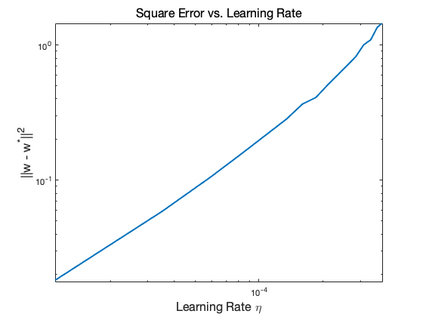
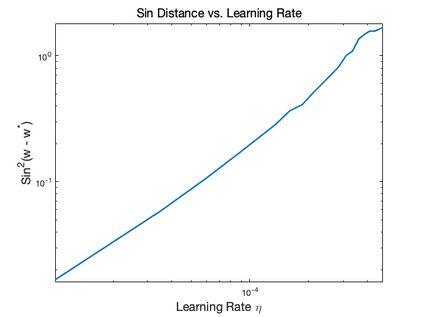
Motivated by the problem of online canonical correlation analysis, we propose the \emph{Stochastic Scaled-Gradient Descent} (SSGD) algorithm for minimizing the expectation of a stochastic function over a generic Riemannian manifold. SSGD generalizes the idea of projected stochastic gradient descent and allows the use of scaled stochastic gradients instead of stochastic gradients. In the special case of a spherical constraint, which arises in generalized eigenvector problems, we establish a nonasymptotic finite-sample bound of $\sqrt{1/T}$, and show that this rate is minimax optimal, up to a polylogarithmic factor of relevant parameters. On the asymptotic side, a novel trajectory-averaging argument allows us to achieve local asymptotic normality with a rate that matches that of Ruppert-Polyak-Juditsky averaging. We bring these ideas together in an application to online canonical correlation analysis, deriving, for the first time in the literature, an optimal one-time-scale algorithm with an explicit rate of local asymptotic convergence to normality. Numerical studies of canonical correlation analysis are also provided for synthetic data.
翻译:以在线光学相关关系分析问题为动力,我们建议使用 emph{Stochistic Scottic Scalled-Gradient Fround} (SSGD) 算法, 最大限度地降低对通用里曼式多元体的随机功能的期望值。 SSGD 概括了预测随机梯度梯度下降的概念, 并允许使用缩放的随机梯度梯度, 而不是随机梯度梯度。 在球体约束的特殊情况下, 产生于普遍的基因质问题, 我们设置了一个非抽吸定的定量定额( $\ sqrt{1/T} ), 并显示这一速率是小型最大最理想的, 最高可达相关参数的多元性系数。 在无源方面, 新的轨迹稳定论使我们得以实现局部无症状的常态性常态, 其速率与Rupert- Polyak- Juditsky 平均的速率相匹配。 我们将这些想法结合应用到在线的计算机相关关系分析中, 推算出, 在正常的合成水平上, 最优的合成水平的模型分析也提供了一种本地的模型分析。