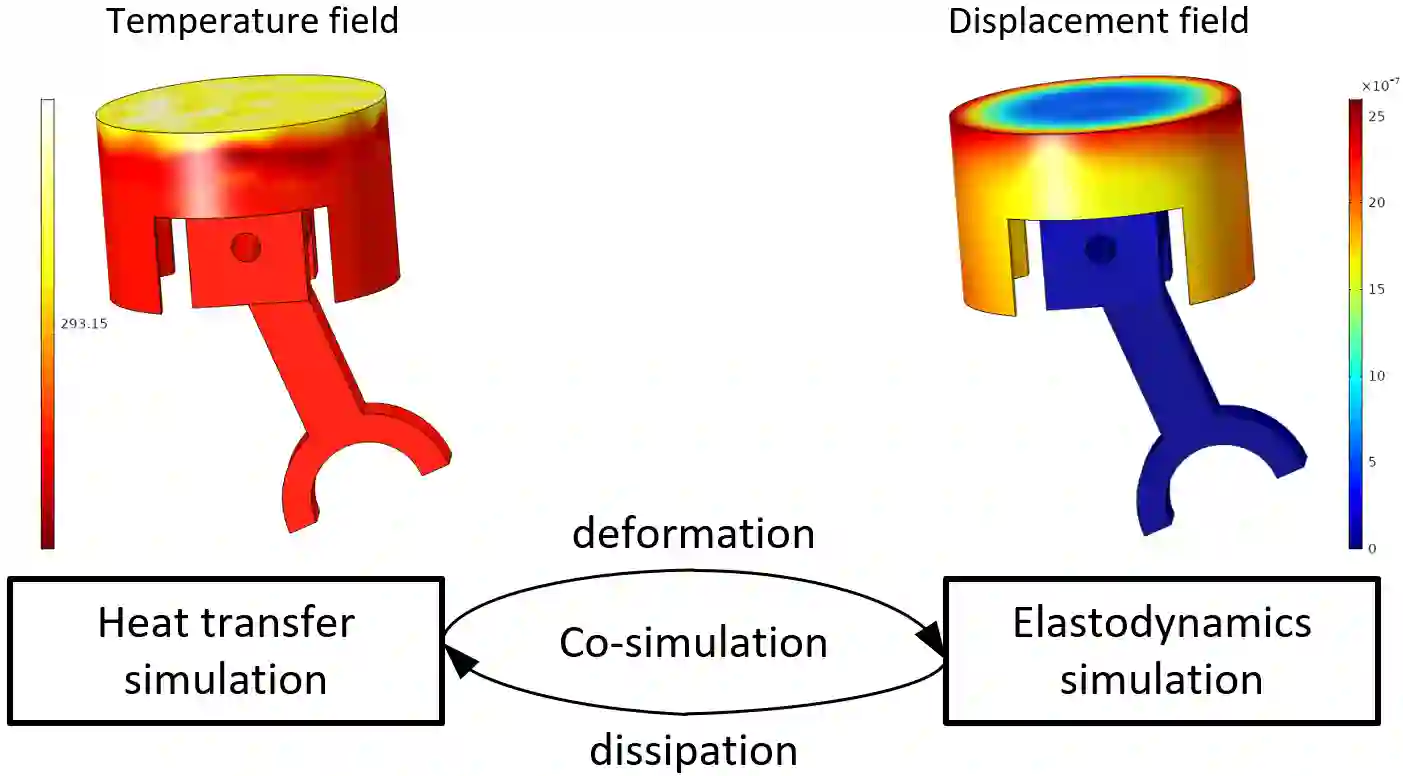
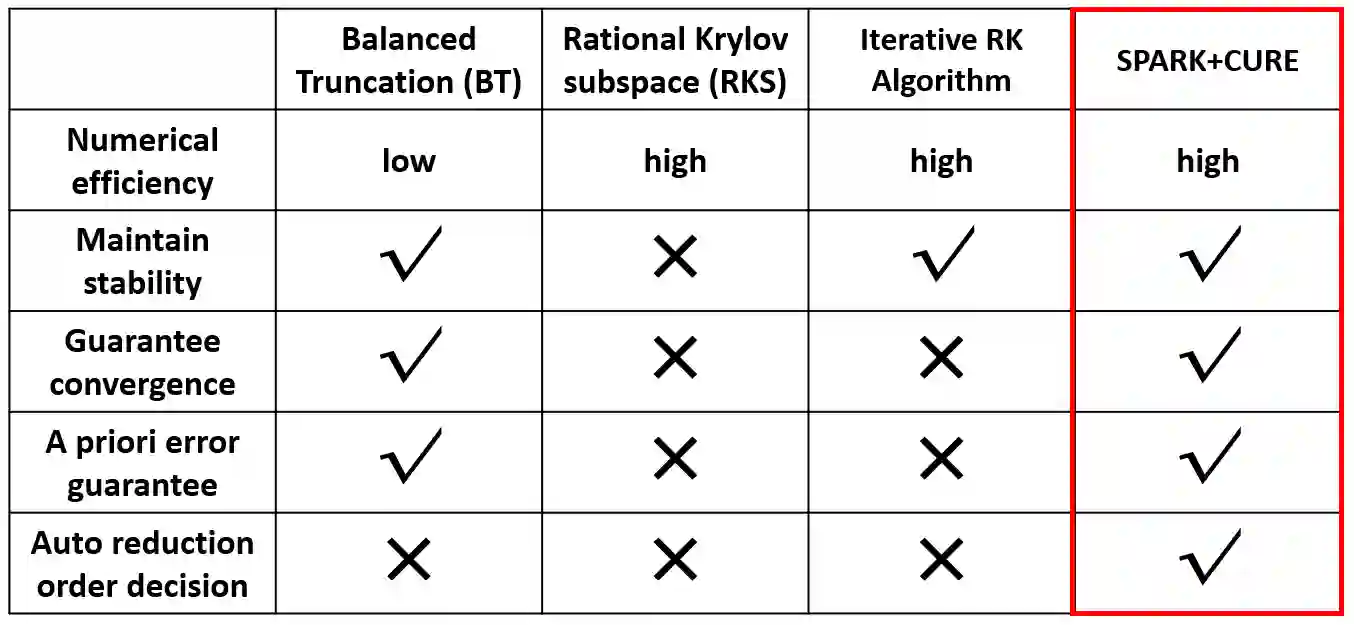
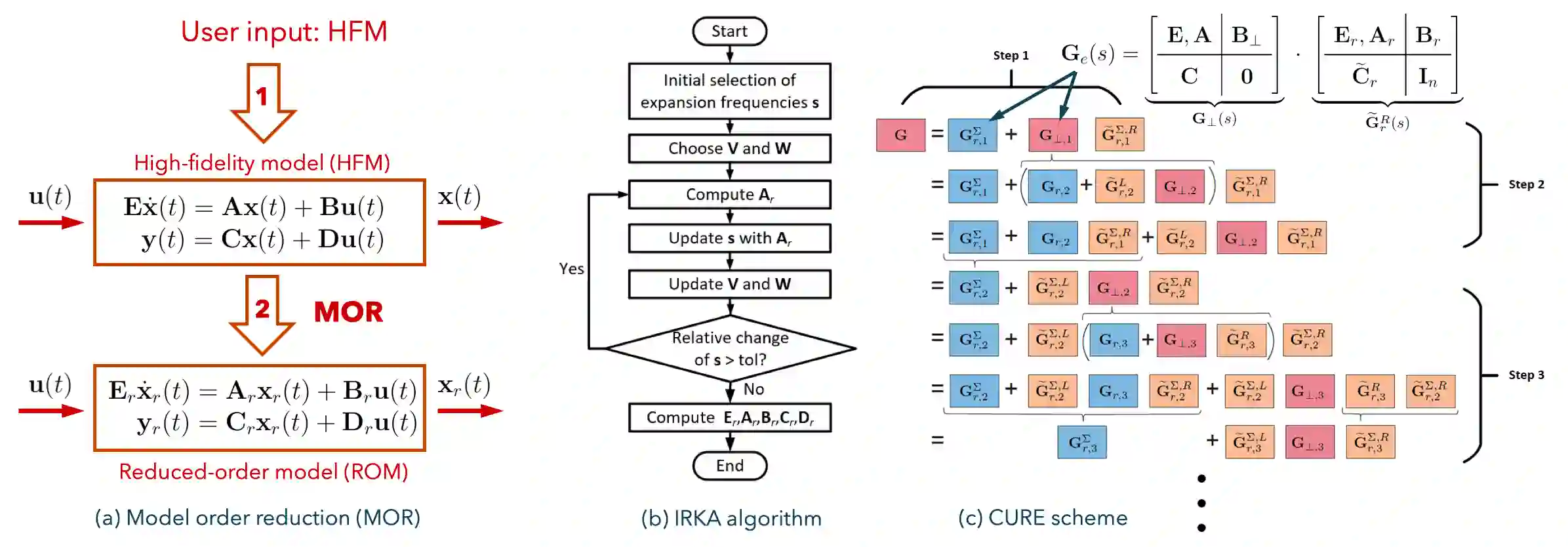
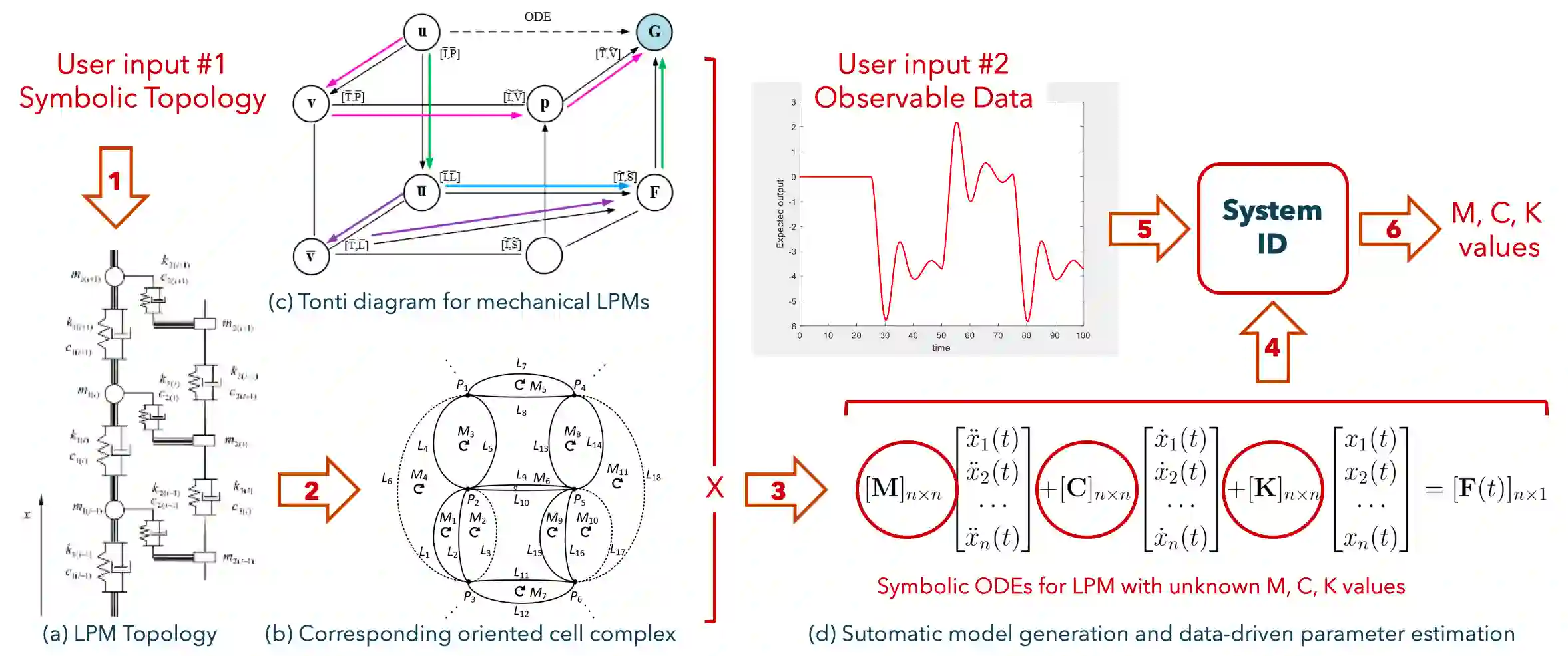
Determining the proper level of details to develop and solve physical models is usually difficult when one encounters new engineering problems. Such difficulty comes from how to balance the time (simulation cost) and accuracy for the physical model simulation afterwards. We propose a framework for automatic development of a family of surrogate models of physical systems that provide flexible cost-accuracy tradeoffs to assist making such determinations. We present both a model-based and a data-driven strategy to generate surrogate models. The former starts from a high-fidelity model generated from first principles and applies a bottom-up model order reduction (MOR) that preserves stability and convergence while providing a priori error bounds, although the resulting reduced-order model may lose its interpretability. The latter generates interpretable surrogate models by fitting artificial constitutive relations to a presupposed topological structure using experimental or simulation data. For the latter, we use Tonti diagrams to systematically produce differential equations from the assumed topological structure using algebraic topological semantics that are common to various lumped-parameter models (LPM). The parameter for the constitutive relations are estimated using standard system identification algorithms. Our framework is compatible with various spatial discretization schemes for distributed parameter models (DPM), and can supports solving engineering problems in different domains of physics.
翻译:当遇到新的工程问题时,通常很难确定开发和解决物理模型的适当细节水平。这种困难来自如何平衡时间(模拟成本)和随后物理模型模拟的准确性。我们提议了一个框架,用于自动开发一系列替代模型的物理系统替代模型,这些模型提供灵活的成本-准确性权衡,以协助作出这种确定。我们提出了一个基于模型和数据驱动的战略,以产生替代模型。前者是从最初原则产生的高纤维模型开始的,采用自下而上的模式减少,既保持稳定性和趋同性,同时又提供先验误差界限。尽管由此形成的减序模型可能会失去其可解释性。后者产生可解释的代孕模型,利用实验或模拟数据将人工构造关系与假设的表层结构相匹配。对于后者,我们使用Tonti图表系统生成假设表层结构的差别方程式,使用各种单式参数模型(LPMM),用于维护稳定性和趋同性差的组合式模型的参数是使用各种标准系统模型的可兼容性模型。我们使用不同空间模型的模型的模型,用来估算各种可比较性模型。