Contamination Bias in Linear Regressions

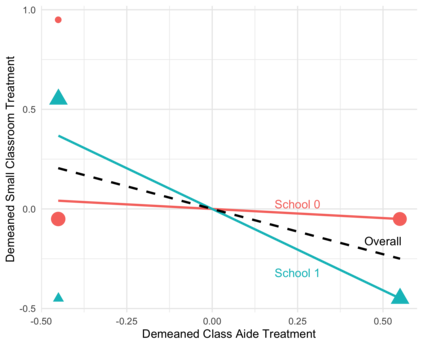
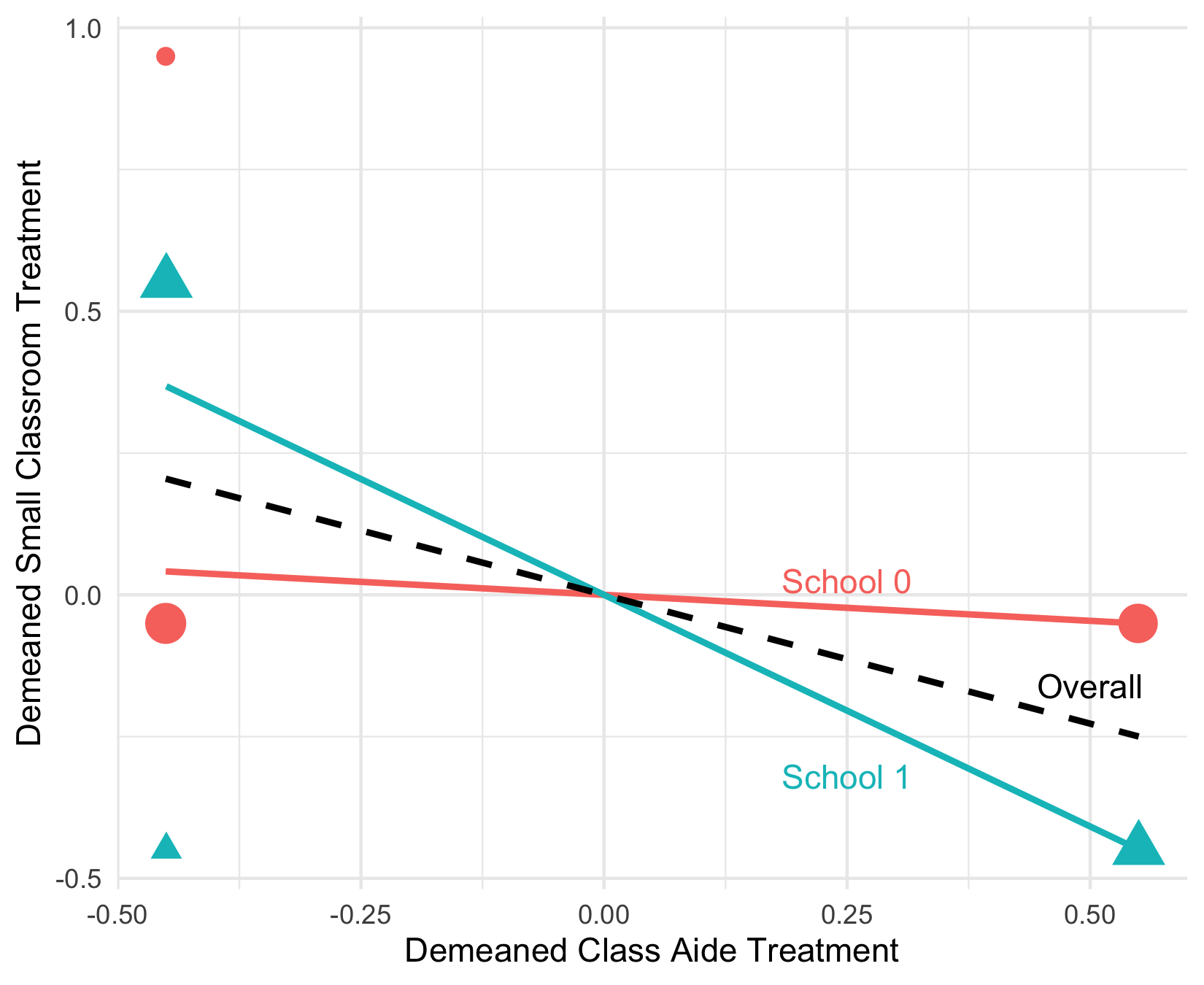
We study the interpretation of regressions with multiple treatments and flexible controls. Such regressions are often used to analyze stratified randomized control trials with multiple intervention arms, to estimate value-added (for, e.g., teachers) with observational data, and to leverage the quasi-random assignment of decision-makers (e.g. bail judges). We show that these regressions generally fail to estimate convex averages of heterogeneous treatment effects, even when the treatments are conditionally randomly assigned and the controls are sufficiently flexible to avoid omitted variables bias. Instead, estimates of each treatment's effects are generally contaminated by a non-convex average of the effects of other treatments. Thus, recent concerns about heterogeneity-induced bias in regressions leveraging potential outcome restrictions (e.g. parallel trends assumptions) also arise with "design-based" identification strategies. We discuss solutions to the contamination bias and propose a new class of efficient estimators of weighted average effects that avoid bias. In a re-analysis of the Project STAR trial, we find minimal bias because treatment effect heterogeneity is largely idiosyncratic. But sizeable contamination bias arises when effect heterogeneity becomes correlated with treatment propensity scores.