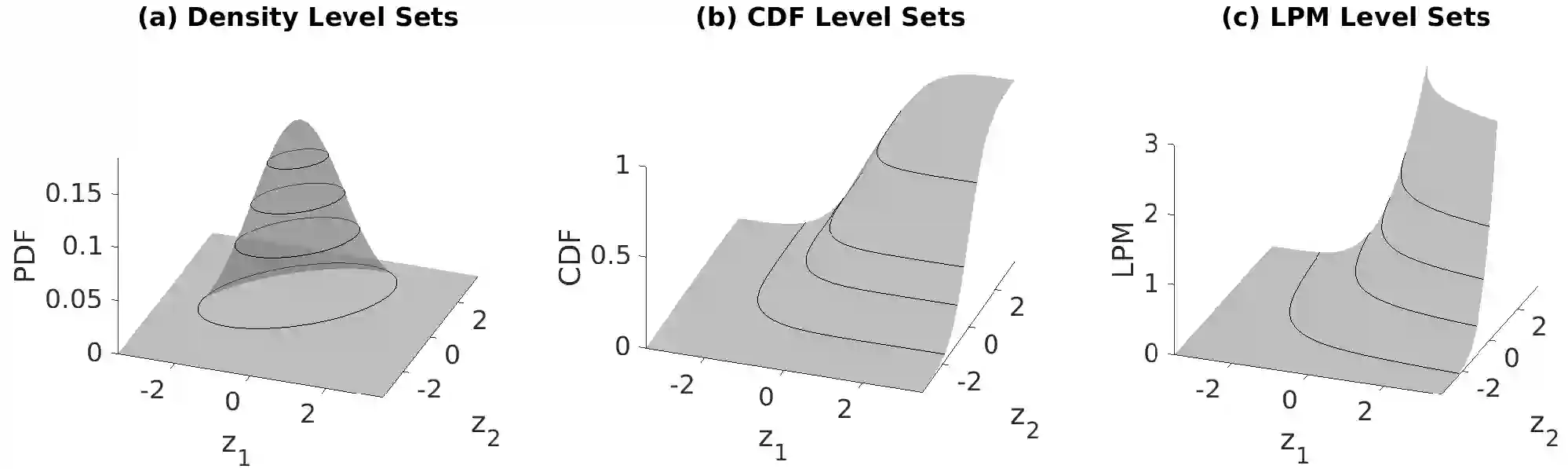
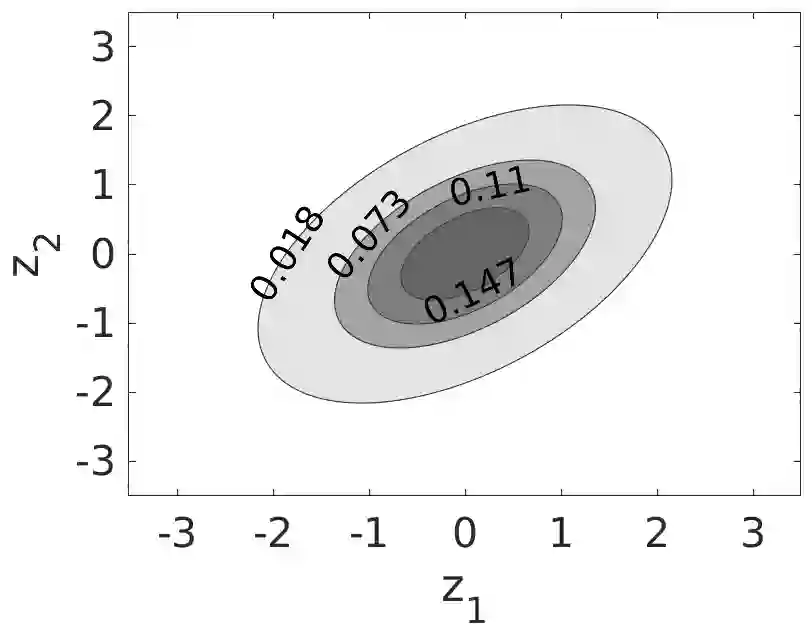
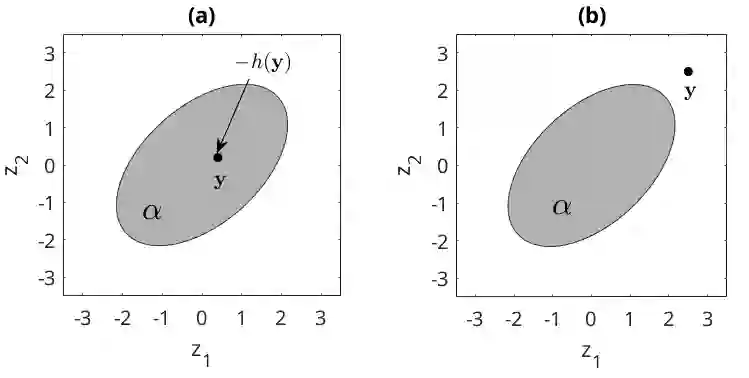
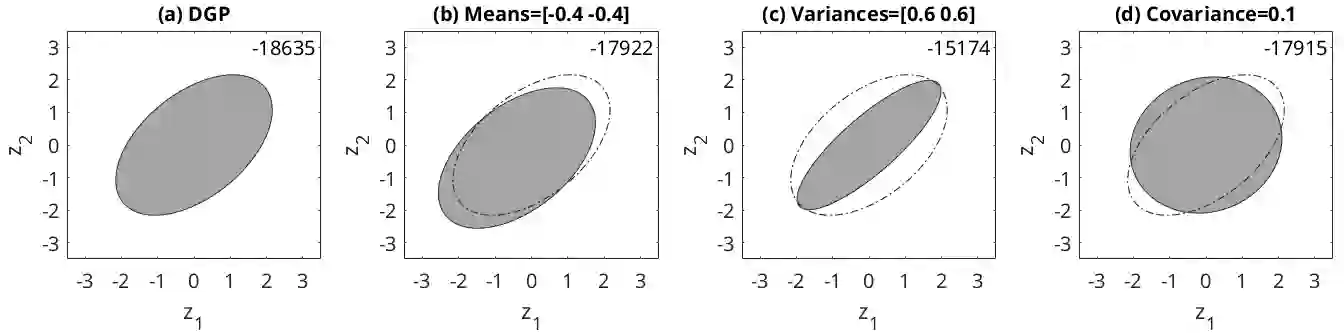
Forecasts of multivariate probability distributions are required for a variety of applications. Scoring rules enable the evaluation of forecast accuracy, and comparison between forecasting methods. We propose a theoretical framework for scoring rules for multivariate distributions, which encompasses the existing quadratic score and multivariate continuous ranked probability score. We demonstrate how this framework can be used to generate new scoring rules. In some multivariate contexts, it is a forecast of a level set that is needed, such as a density level set for anomaly detection or the level set of the cumulative distribution as a measure of risk. This motivates consideration of scoring functions for such level sets. For univariate distributions, it is well-established that the continuous ranked probability score can be expressed as the integral over a quantile score. We show that, in a similar way, scoring rules for multivariate distributions can be decomposed to obtain scoring functions for level sets. Using this, we present scoring functions for different types of level set, including density level sets and level sets for cumulative distributions. To compute the scores, we propose a simple numerical algorithm. We perform a simulation study to support our proposals, and we use real data to illustrate usefulness for forecast combining and CoVaR estimation.
翻译:各种应用都需要多变量概率分布的预测。 排序规则允许对预测准确性进行评估, 并比较预测方法。 我们为多变量分布的评分规则提议了一个理论框架, 其中包括现有的四级评分和多变量连续评分的概率分数。 我们演示了如何使用这个框架来产生新的评分规则。 在一些多变量背景下, 这是对需要的等级的预测, 比如为异常检测设定的密度水平或累积分布水平设定的密度, 作为风险的衡量标准。 这促使考虑这些等级组的评分函数。 对于单位分布, 我们非常确定连续排名概率评分可以表示成一个四分分分数的完整分数。 我们以类似的方式显示, 多变量分布的评分规则可以被拆分, 以获得等级组的评分功能。 使用这个方法, 我们为不同等级组的评分设置, 包括密度等级组和累积分布的等级组。 为了计算得分, 我们建议一个简单的数值算法。 我们进行模拟研究, 以显示我们的预测结果, 并使用我们用真实的数据来说明。