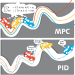
Finite-time Lyapunov exponents (FTLEs) provide a powerful approach to compute time-varying analogs of invariant manifolds in unsteady fluid flow fields. These manifolds are useful to visualize the transport mechanisms of passive tracers advecting with the flow. However, many vehicles and mobile sensors are not passive, but are instead actuated according to some intelligent trajectory planning or control law; for example, model predictive control and reinforcement learning are often used to design energy-efficient trajectories in a dynamically changing background flow. In this work, we investigate the use of FTLE on such controlled agents to gain insight into optimal transport routes for navigation in known unsteady flows. We find that these controlled FTLE (cFTLE) coherent structures separate the flow field into different regions with similar costs of transport to the goal location. These separatrices are functions of the planning algorithm's hyper-parameters, such as the optimization time horizon and the cost of actuation. Computing the invariant sets and manifolds of active agent dynamics in dynamic flow fields is useful in the context of robust motion control, hyperparameter tuning, and determining safe and collision-free trajectories for autonomous systems. Moreover, these cFTLE structures provide insight into effective deployment locations for mobile agents with actuation and energy constraints to traverse the ocean or atmosphere.
翻译:短时Lyapunov指数(FTLE)为计算非稳态流场中不变流形的时变模拟提供了强大的方法。这些流形可用于可视化被流动移动的被动示踪器的传输机制。然而,许多车辆和移动传感器不是被动的,而是根据一些智能轨迹规划或控制法则进行驱动;例如,模型预测控制和强化学习经常用于在动态变化的背景流中设计节能轨迹。在本研究中,我们调查了在这些受控制的代理上使用FTLE来获取关于在已知非稳态流中的最优传输路径的见解。我们发现,这些受控FTLE(cFTLE)相干结构将流场分为具有相似到达目标位置传输成本的不同区域。这些分界线是计划算法的超参数的函数,例如优化时间、作用成本等。计算动态流场中主动代理动力学的不变集和流形对于强健运动控制、超参数调整以及确定自主系统的安全和无碰撞轨迹是有用的。此外,这些cFTLE结构为具有作用和能量约束的移动代理的有效部署位置提供了洞察力,以遍历海洋或大气。