Majorization Minimization Methods for Distributed Pose Graph Optimization

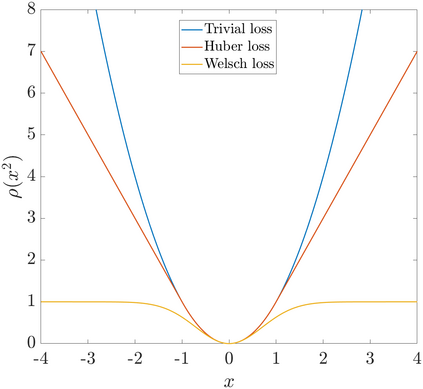
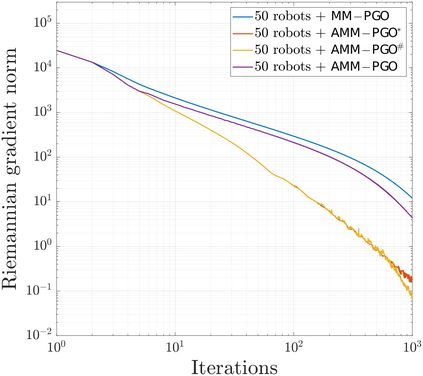
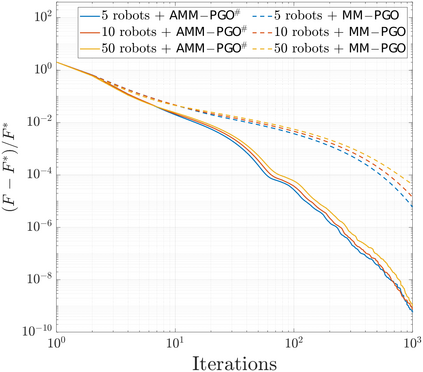
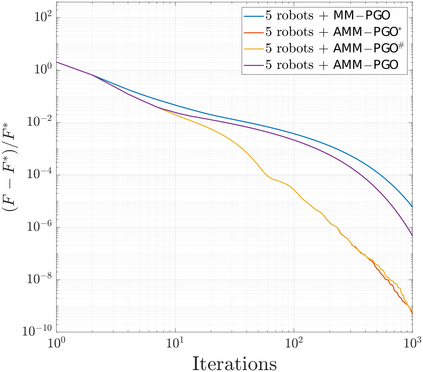
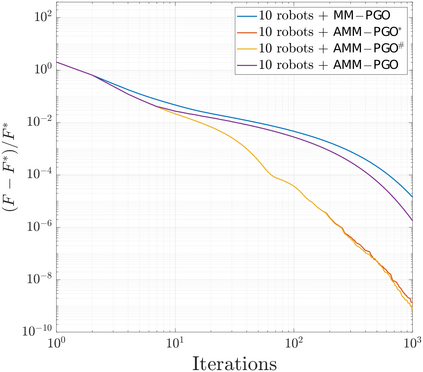
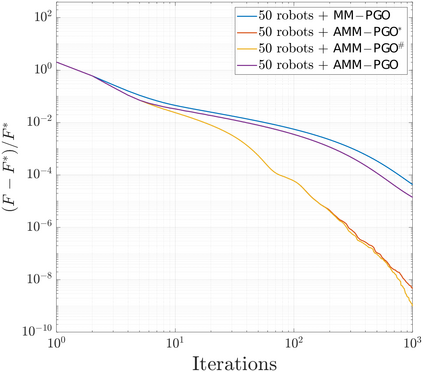
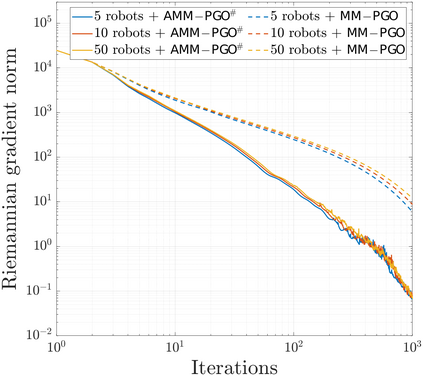
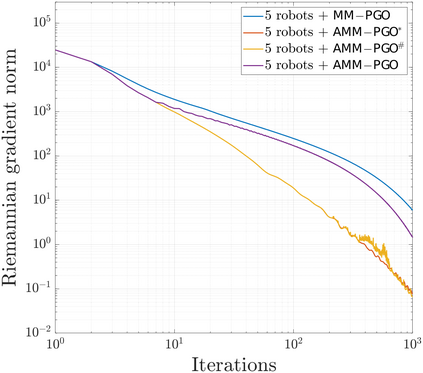
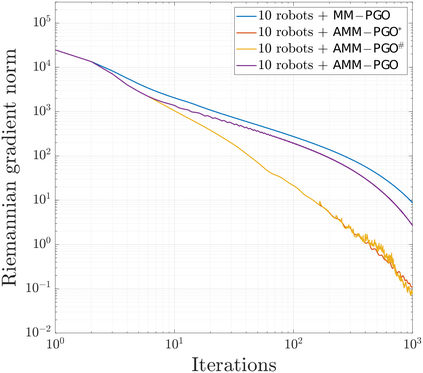
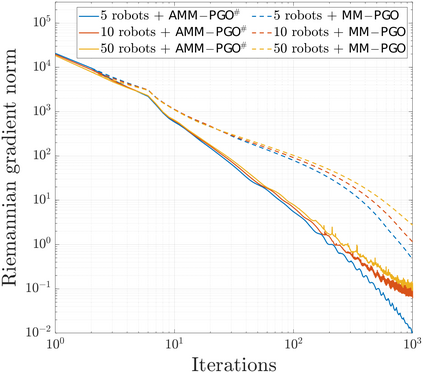
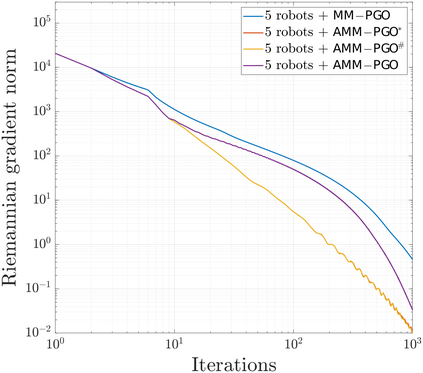
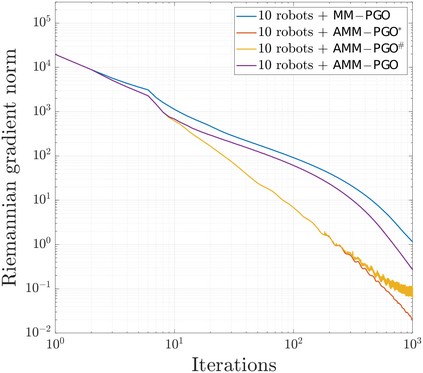
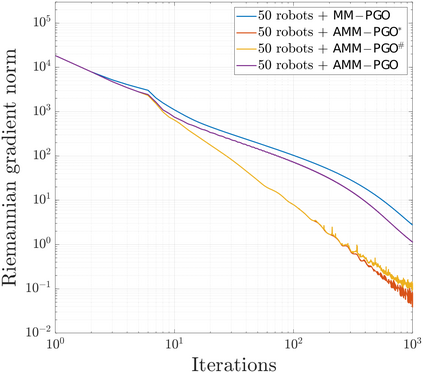
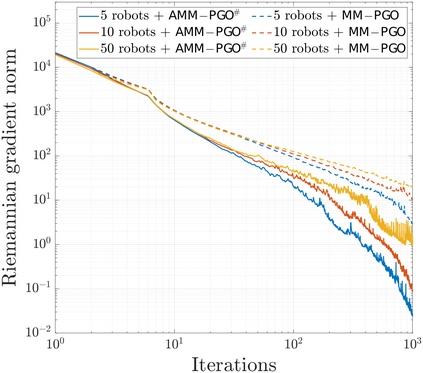
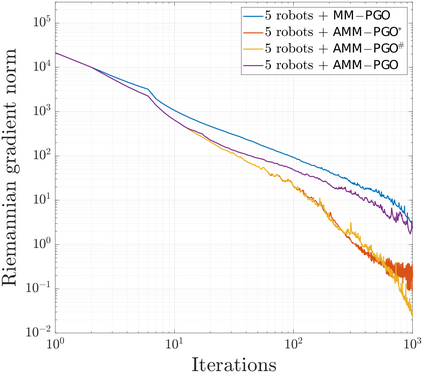
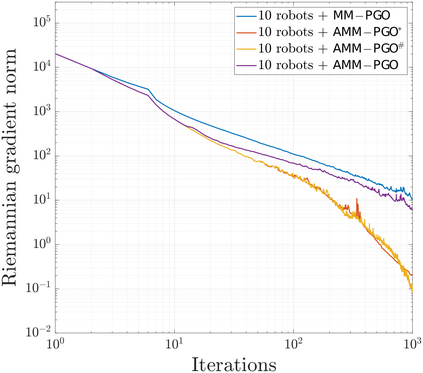
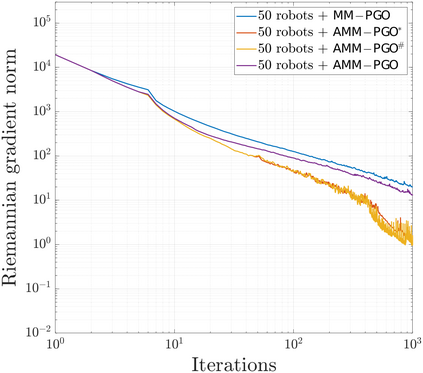
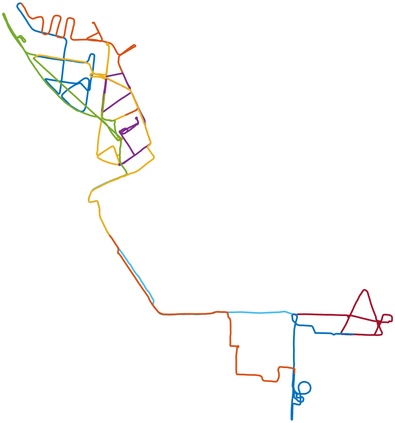
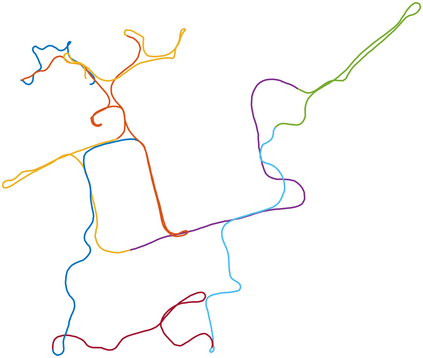
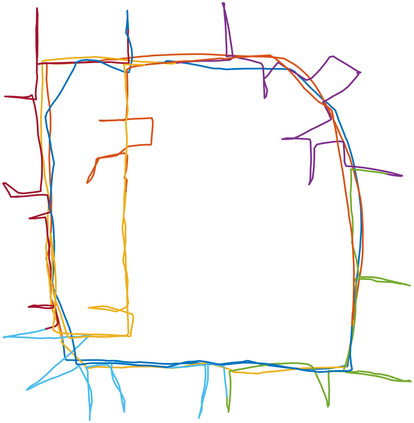
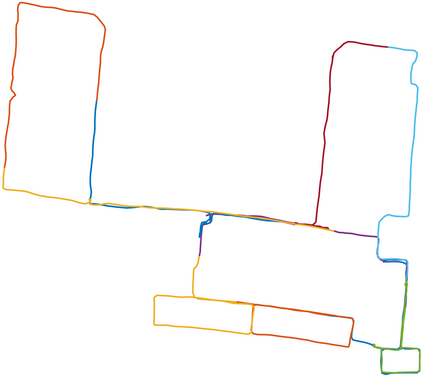
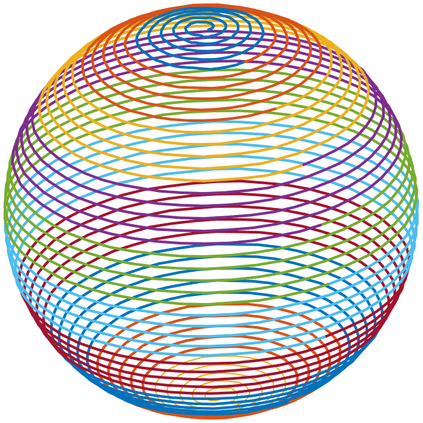
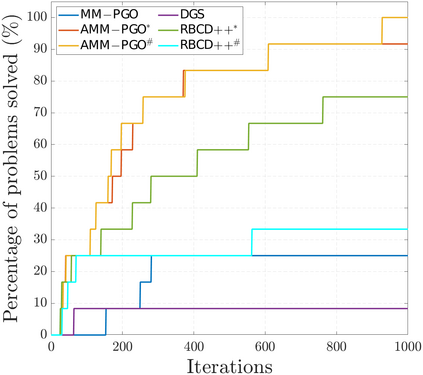
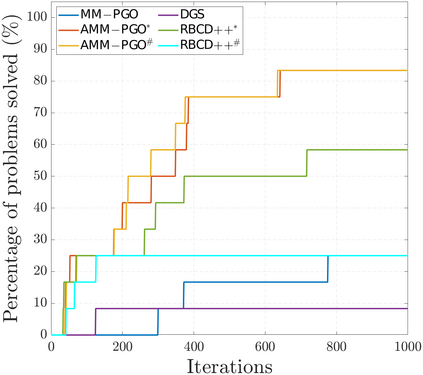
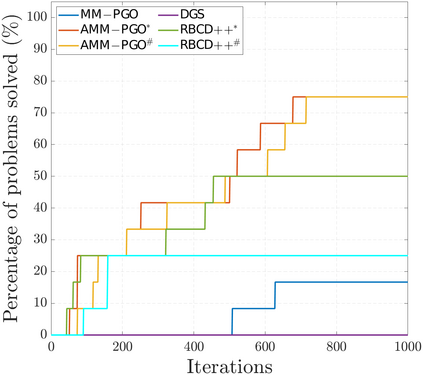
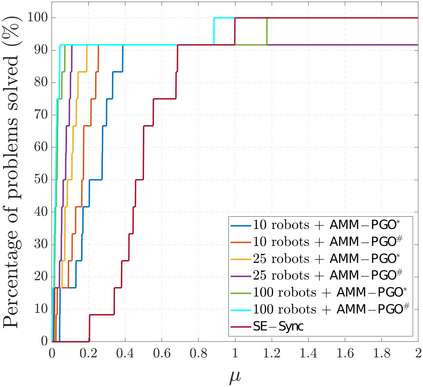
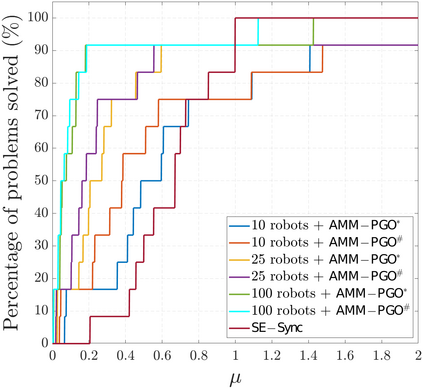
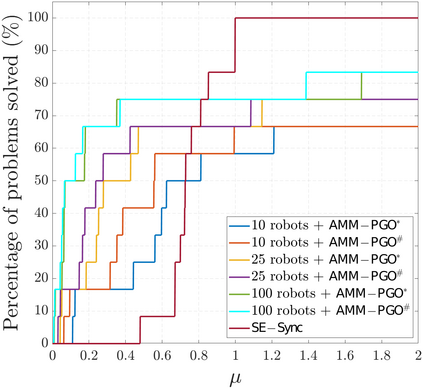
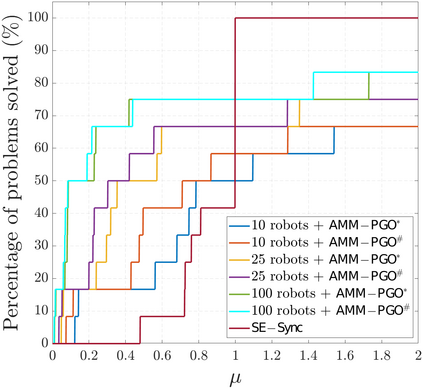
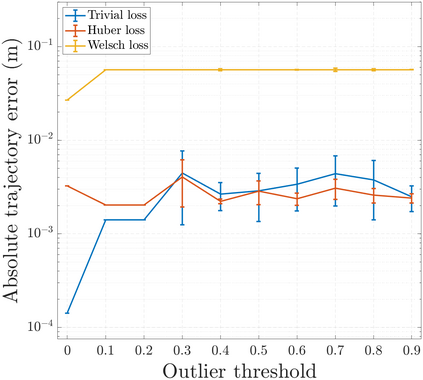
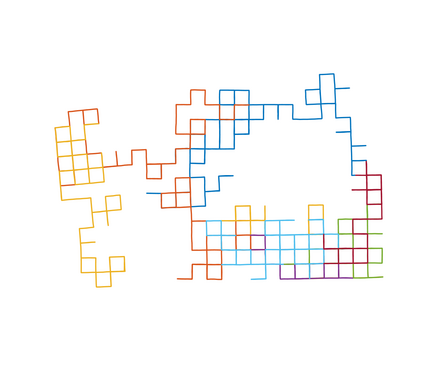We consider the problem of distributed pose graph optimization (PGO) that has important applications in multi-robot simultaneous localization and mapping (SLAM). We propose the majorization minimization (MM) method for distributed PGO ($\mathsf{MM\!\!-\!\!PGO}$) that applies to a broad class of robust loss kernels. The $\mathsf{MM\!\!-\!\!PGO}$ method is guaranteed to converge to first-order critical points under mild conditions. Furthermore, noting that the $\mathsf{MM\!\!-\!\!PGO}$ method is reminiscent of proximal methods, we leverage Nesterov's method and adopt adaptive restarts to accelerate convergence. The resulting accelerated MM methods for distributed PGO -- both with a master node in the network ($\mathsf{AMM\!\!-\!\!PGO}^*$) and without ($\mathsf{AMM\!\!-\!\!PGO}^{#}$) -- have faster convergence in contrast to the $\mathsf{MM\!\!-\!\!PGO}$ method without sacrificing theoretical guarantees. In particular, the $\mathsf{AMM\!\!-\!\!PGO}^{#}$ method, which needs no master node and is fully decentralized, features a novel adaptive restart scheme and has a rate of convergence comparable to that of the $\mathsf{AMM\!\!-\!\!PGO}^*$ method using a master node to aggregate information from all the other nodes. The efficacy of this work is validated through extensive applications to 2D and 3D SLAM benchmark datasets and comprehensive comparisons against existing state-of-the-art methods, indicating that our MM methods converge faster and result in better solutions to distributed PGO.