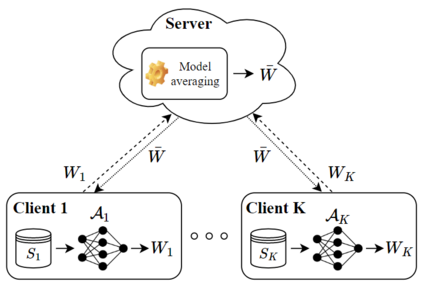
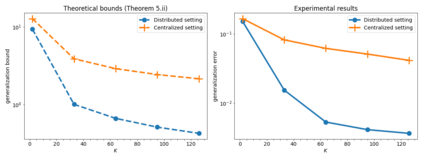
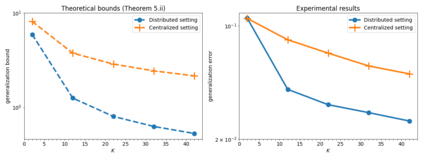
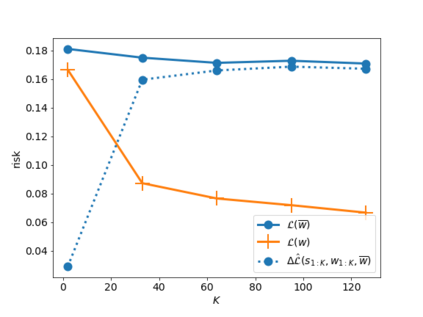
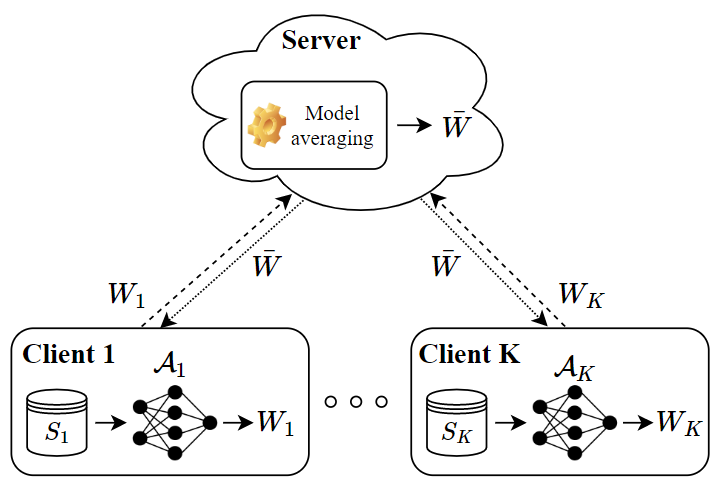
In this paper, we use tools from rate-distortion theory to establish new upper bounds on the generalization error of statistical distributed learning algorithms. Specifically, there are $K$ clients whose individually chosen models are aggregated by a central server. The bounds depend on the compressibility of each client's algorithm while keeping other clients' algorithms un-compressed, and leverage the fact that small changes in each local model change the aggregated model by a factor of only $1/K$. Adopting a recently proposed approach by Sefidgaran et al., and extending it suitably to the distributed setting, this enables smaller rate-distortion terms which are shown to translate into tighter generalization bounds. The bounds are then applied to the distributed support vector machines (SVM), suggesting that the generalization error of the distributed setting decays faster than that of the centralized one with a factor of $\mathcal{O}(\log(K)/\sqrt{K})$. This finding is validated also experimentally. A similar conclusion is obtained for a multiple-round federated learning setup where each client uses stochastic gradient Langevin dynamics (SGLD).
翻译:在本文中,我们使用调试率理论的工具来为统计分布式学习算法的普及错误设定新的上限。 具体地说, 有K美元客户的客户个人选择的模型由中央服务器汇总。 这些界限取决于每个客户的算法的压缩, 同时保持其他客户的算法不受压缩, 并充分利用以下事实,即每个本地模型的微小变化仅以1/ K$的系数改变综合模型。 采用Sefidgaran 等人最近提出的一种方法, 并将其扩展为适合分布式设置, 这样可以使较小的调试率术语被显示为更紧凑的通用界限。 这些界限随后被应用到分布式的辅助矢量机( SVM), 这表明分布式设置的普遍误差比集中式的差快, 系数为$\mathcal{O} (\log (K)/\qrt{K} 。 这一发现也得到实验性验证。 每个客户都使用渐变的梯状学习设置, 获得类似的结论。