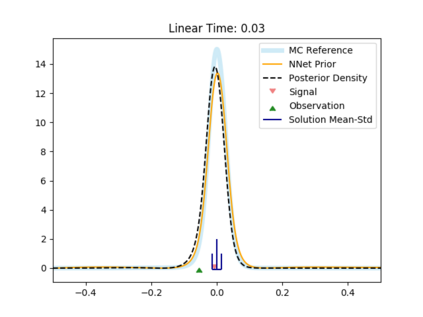
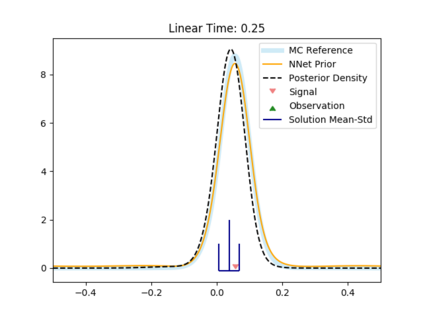
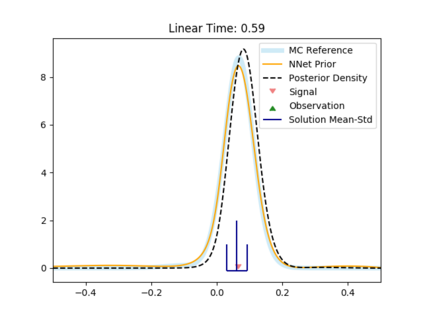
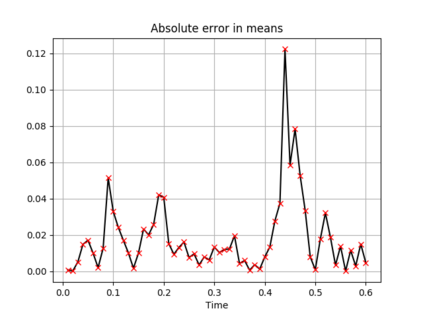
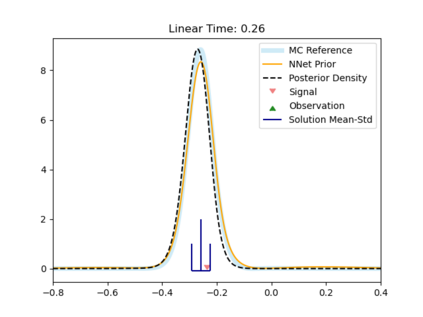
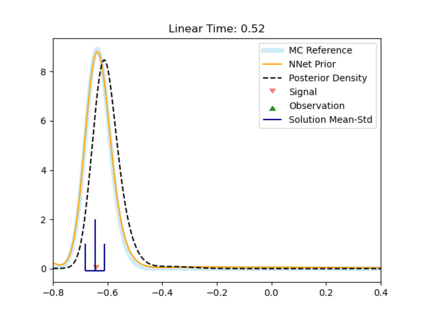
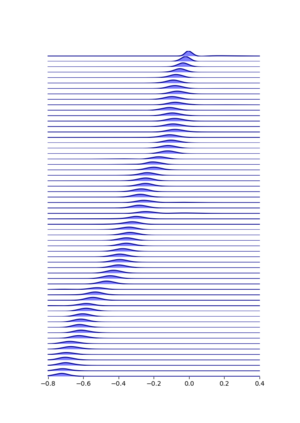
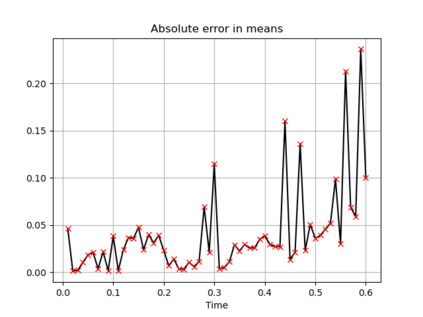
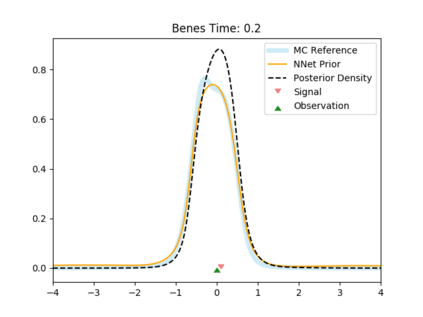
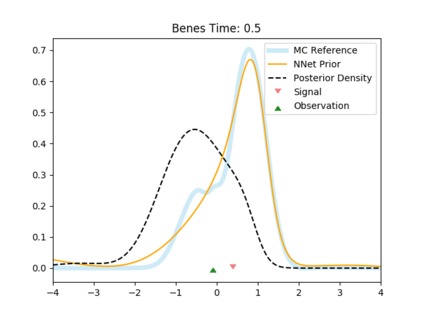
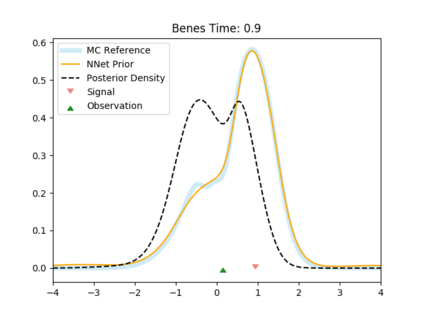
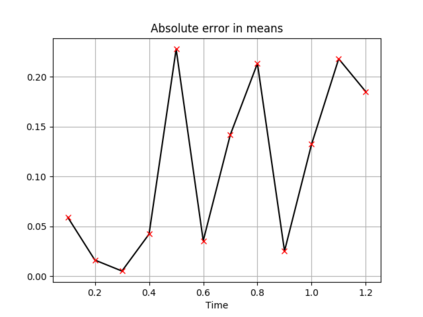
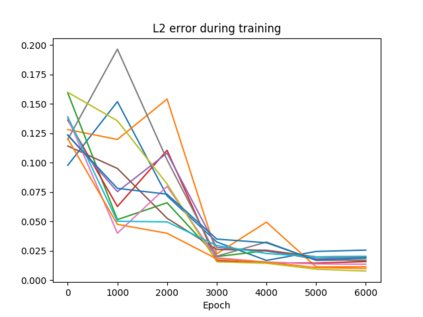
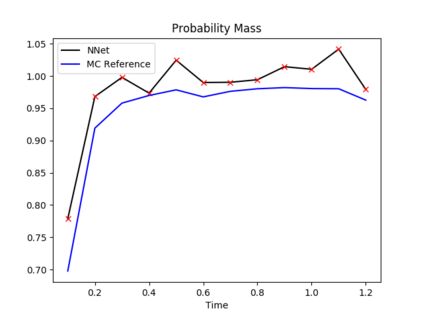
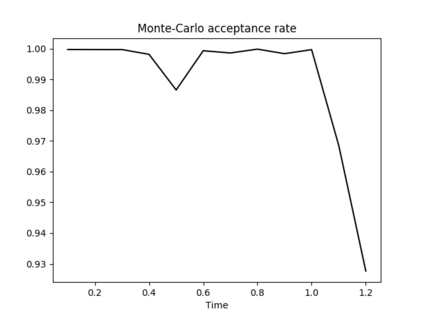
The filtering equations govern the evolution of the conditional distribution of a signal process given partial, and possibly noisy, observations arriving sequentially in time. Their numerical approximation plays a central role in many real-life applications, including numerical weather prediction, finance and engineering. One of the classical approaches to approximate the solution of the filtering equations is to use a PDE inspired method, called the splitting-up method, initiated by Gyongy, Krylov, LeGland, among other contributors. This method, and other PDE based approaches, have particular applicability for solving low-dimensional problems. In this work we combine this method with a neural network representation. The new methodology is used to produce an approximation of the unnormalised conditional distribution of the signal process. We further develop a recursive normalisation procedure to recover the normalised conditional distribution of the signal process. The new scheme can be iterated over multiple time steps whilst keeping its asymptotic unbiasedness property intact. We test the neural network approximations with numerical approximation results for the Kalman and Benes filter.
翻译:过滤方程式管理信号进程有条件分布的演进, 给部分且可能吵闹的观测时间依次到来。 它们的数字近似值在许多实际应用中起着核心作用, 包括数字天气预测、 金融和工程。 接近过滤方程解决方案的典型方法之一是使用一种PDE 启发法, 称为分裂法, 由 Gyongy、 Krylov、 LeGland 和其他贡献者共同发起。 这种方法以及其他基于 PDE 的方法, 特别适用于解决低维度问题。 在这项工作中, 我们将此方法与神经网络的表示法结合起来。 新方法被用于生成信号进程非正常有条件分布的近似值。 我们进一步开发循环正常化程序, 以恢复信号进程的正常有条件分布 。 新的方案可以在多个时间步骤中循环, 同时保持其无损的公正性属性的完整。 我们测试神经网络近似值, 并测试 Kalman 和 Benes 过滤器的数字近似值结果 。