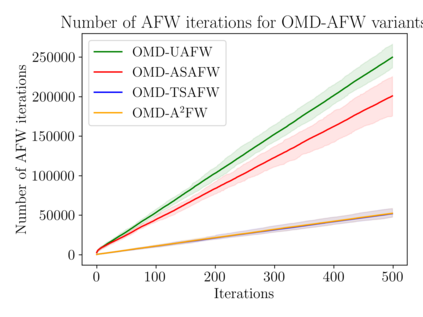
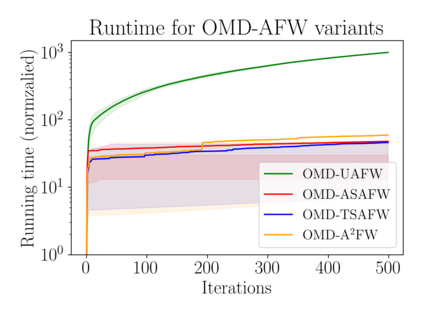
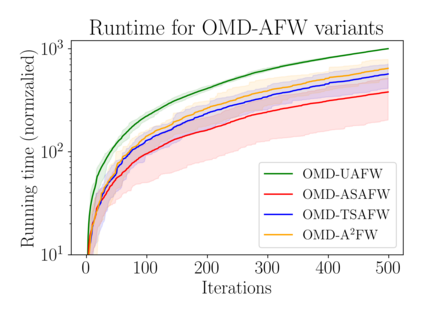
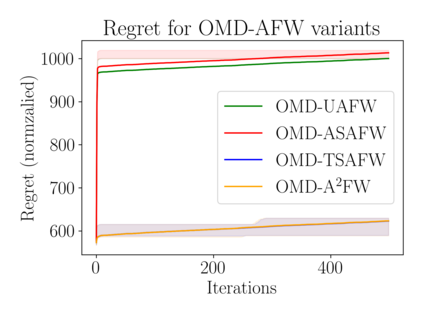
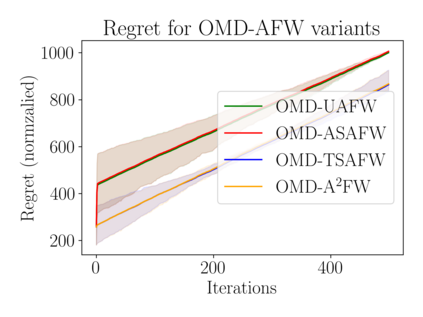
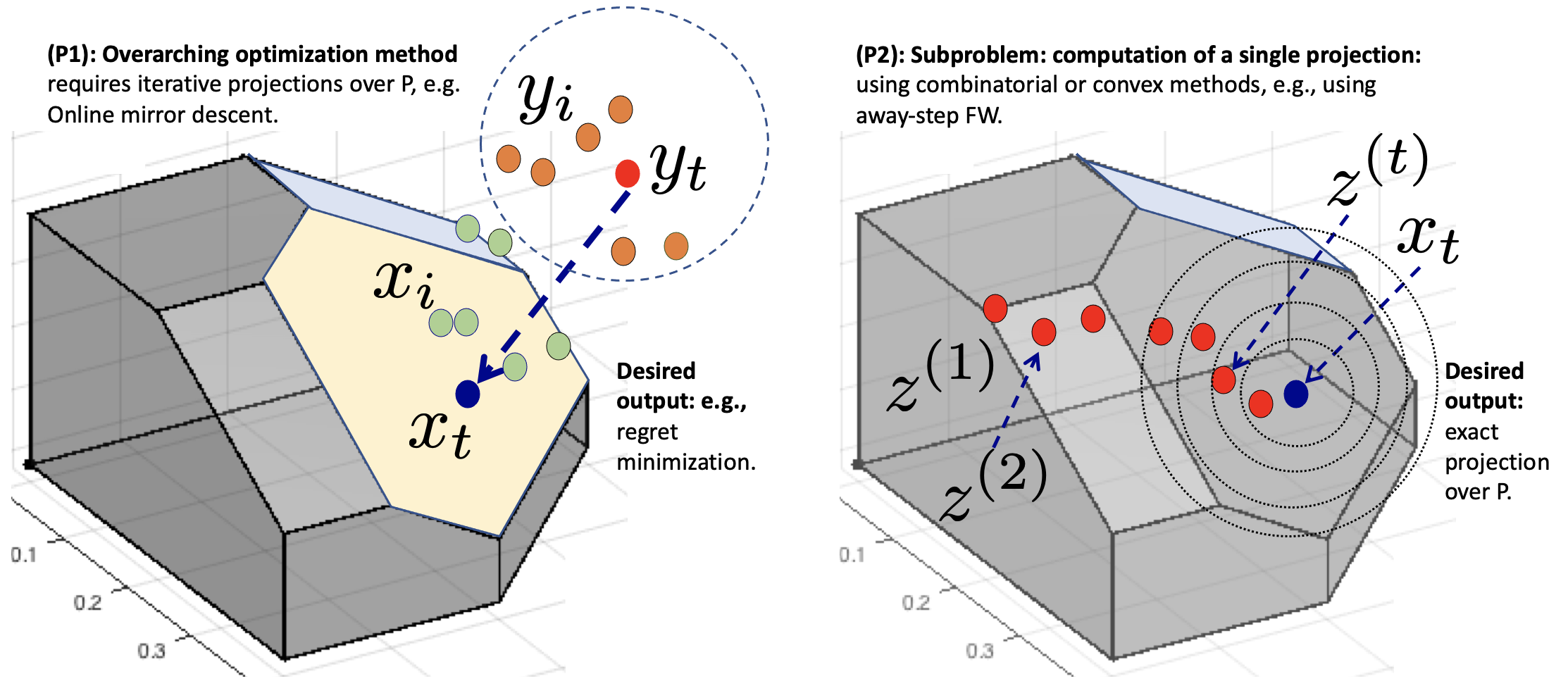
Optimization algorithms such as projected Newton's method, FISTA, mirror descent and its variants enjoy near-optimal regret bounds and convergence rates, but suffer from a computational bottleneck of computing "projections'' in potentially each iteration (e.g., $O(T^{1/2})$ regret of online mirror descent). On the other hand, conditional gradient variants solve a linear optimization in each iteration, but result in suboptimal rates (e.g., $O(T^{3/4})$ regret of online Frank-Wolfe). Motivated by this trade-off in runtime v/s convergence rates, we consider iterative projections of close-by points over widely-prevalent submodular base polytopes $B(f)$. We develop a toolkit to speed up the computation of projections using both discrete and continuous perspectives. We subsequently adapt the away-step Frank-Wolfe algorithm to use this information and enable early termination. For the special case of cardinality based submodular polytopes, we improve the runtime of computing certain Bregman projections by a factor of $\Omega(n/\log(n))$. Our theoretical results show orders of magnitude reduction in runtime in preliminary computational experiments.
翻译:最佳化算法,如预测牛顿法、FISTA、镜底及其变种等优化算法,享有接近最佳的遗憾度和趋同率,但受到计算“预测”的计算瓶颈的困扰(例如,O(T ⁇ 1/2})美元对在线镜色下降的遗憾)。另一方面,有条件的梯度变方程式解决了每个循环的线性优化,但导致亚最佳率(例如,美元(T ⁇ 3/4})美元对在线弗兰克-沃夫的遗憾)。受这种运行时间对合并率的权衡驱动,我们考虑对“预测”的潜在每种循环(例如,$O(T ⁇ 1/2})美元对在线镜状下降的近点进行反复预测(例如,美元(T ⁇ 3/4}) 。我们开发了一套工具,用离散和连续的视角加速计算预测。我们随后调整了离位法-沃夫算法算法,以使用这一信息并实现早期终止。对于基于基底基底基质的亚模多式多式多端的特例的特殊案例,我们改进了对亚基数计算结果的运行时时程/计算结果。