Strategic investments in multi-stage General Lotto games

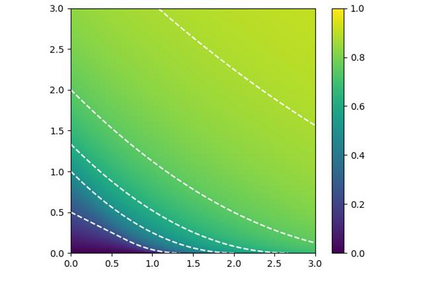
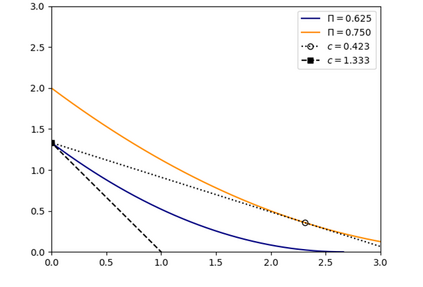
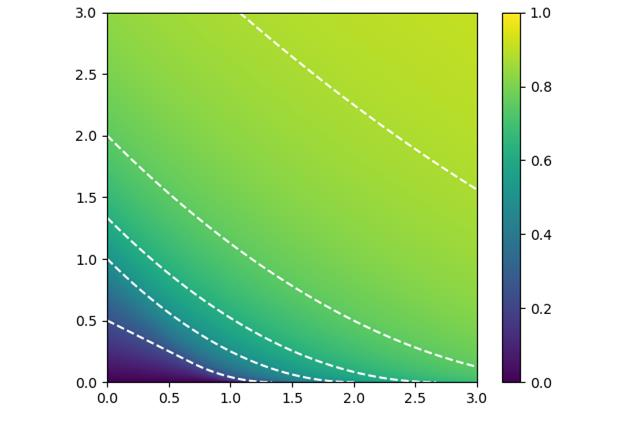
In adversarial interactions, one is often required to make strategic decisions over multiple periods of time, wherein decisions made earlier impact a player's competitive standing as well as how choices are made in later stages. In this paper, we study such scenarios in the context of General Lotto games, which models the competitive allocation of resources over multiple battlefields between two players. We propose a two-stage formulation where one of the players has reserved resources that can be strategically pre-allocated across the battlefields in the first stage. The pre-allocation then becomes binding and is revealed to the other player. In the second stage, the players engage by simultaneously allocating their real-time resources against each other. The main contribution in this paper provides complete characterizations of equilibrium payoffs in the two-stage game, revealing the interplay between performance and the amount of resources expended in each stage of the game. We find that real-time resources are at least twice as effective as pre-allocated resources. We then determine the player's optimal investment when there are linear costs associated with purchasing each type of resource before play begins, and there is a limited monetary budget.