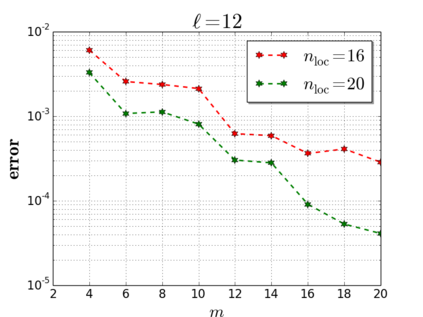
This paper is concerned with error estimates of the fully discrete generalized finite element method (GFEM) with optimal local approximation spaces for solving elliptic problems with heterogeneous coefficients. The local approximation spaces are constructed using eigenvectors of local eigenvalue problems solved by the finite element method on some sufficiently fine mesh with mesh size $h$. The error bound of the discrete GFEM approximation is proved to converge as $h\rightarrow 0$ towards that of the continuous GFEM approximation, which was shown to decay nearly exponentially in previous works. Moreover, even for fixed mesh size $h$, a nearly exponential rate of convergence of the local approximation errors with respect to the dimension of the local spaces is established. An efficient and accurate method for solving the discrete eigenvalue problems is proposed by incorporating the discrete $A$-harmonic constraint directly into the eigensolver. Numerical experiments are carried out to confirm the theoretical results and to demonstrate the effectiveness of the method.
翻译:本文涉及完全离散的通用有限要素方法(GFEM)的误差估计,该方法具有解决异差系数的局部近似空间,当地近似空间的构建使用以一定的元素方法解决的本地异质值问题的分解器,该方法在某种相当精细的网格中以美元为单位解决当地异质值问题。离散的GFEM近点的误差被证明为美元/立方美元/美元,与连续的GFEM近似点的误差相趋同,该近似点在以往的工程中几乎呈指数性衰减。此外,即使固定的网格大小为$/h美元,当地近似差差差与当地空间维度的趋同率也几乎是指数化的。通过将离散值$/美元-调和度约束直接纳入乙质体,可以提出解决离电子异值问题的有效和准确的方法。进行了实验,以证实理论结果并证明该方法的有效性。