An overlapping splitting double sweep method for the Helmholtz equation

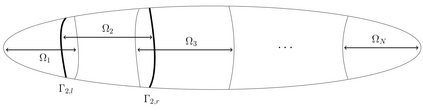
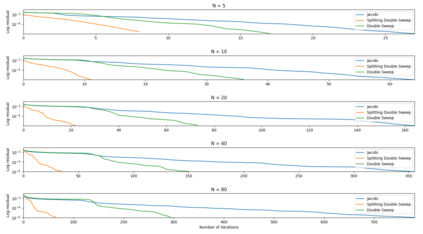
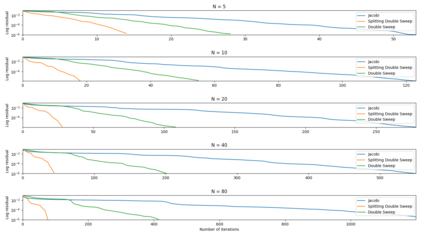
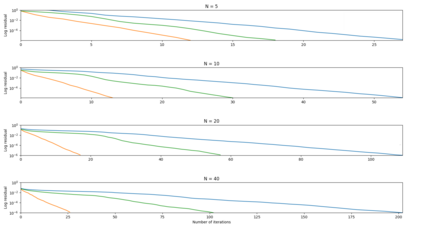
We consider the domain decomposition method approach to solve the Helmholtz equation. Double sweep based approaches for overlapping decompositions are presented. In particular, we introduce an overlapping splitting double sweep (OSDS) method valid for any type of interface boundary conditions. Despite the fact that first order interface boundary conditions are used, the OSDS method demonstrates good stability properties with respect to the number of subdomains and the frequency even for heterogeneous media. In this context, convergence is improved when compared to the double sweep methods in Nataf et al. (1997) and Vion et al. (2014, 2016} for all of our test cases: waveguide, open cavity and wedge problems.