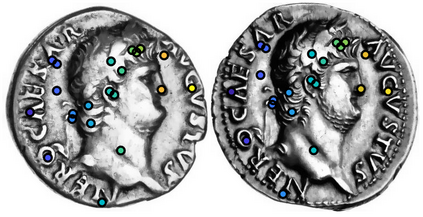
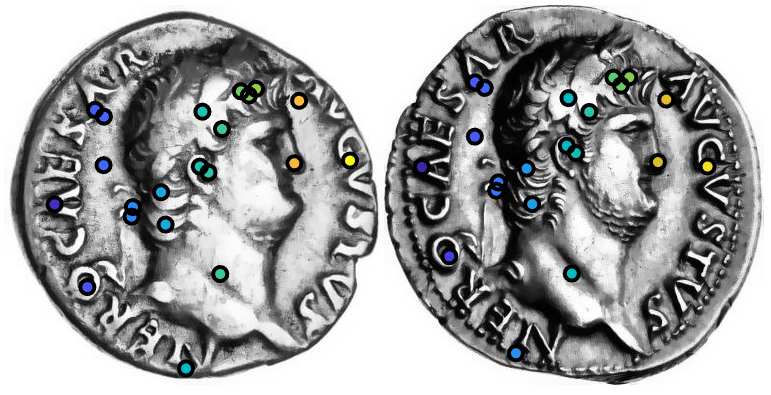
Clustering in high-dimensions poses many statistical challenges. While traditional distance-based clustering methods are computationally feasible, they lack probabilistic interpretation and rely on heuristics for estimation of the number of clusters. On the other hand, probabilistic model-based clustering techniques often fail to scale and devising algorithms that are able to effectively explore the posterior space is an open problem. Based on recent developments in Bayesian distance-based clustering, we propose a hybrid solution that entails defining a likelihood on pairwise distances between observations. The novelty of the approach consists in including both cohesion and repulsion terms in the likelihood, which allows for cluster identifiability. This implies that clusters are composed of objects which have small "dissimilarities" among themselves (cohesion) and similar dissimilarities to observations in other clusters (repulsion). We show how this modelling strategy has interesting connection with existing proposals in the literature as well as a decision-theoretic interpretation. The proposed method is computationally efficient and applicable to a wide variety of scenarios. We demonstrate the approach in a simulation study and an application in digital numismatics.
翻译:在高维度数据的聚类中存在许多统计难题。传统的基于距离的聚类方法是可行的,但缺乏概率解释,并且需要启发式方法来估计聚类数。另一方面,基于概率模型的聚类技术往往难以扩展,并且设计能够有效探索后验空间的算法是一个未解问题。基于贝叶斯距离聚类的最新进展,我们提出了一种混合解决方案——定义一个关于观察值之间成对距离的似然函数。该方法的新颖之处在于,在似然函数中包含了凝聚和排斥项,从而实现了簇的可识别性。这意味着,簇由彼此之间的"不相似度"很小的对象 (凝聚) 以及与其他簇中的观测值具有相似不相似度的对象组成 (排斥)。我们展示了这种建模策略与文献中现有提案的有趣联系,以及决策论解释。所提出的方法计算效率高,并适用于各种情景。我们在一个模拟研究和一个数字货币学应用中演示了该方法的应用。