Multiplying poles to avoid unwanted points in root finding and optimization

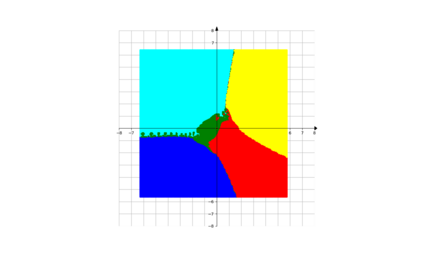
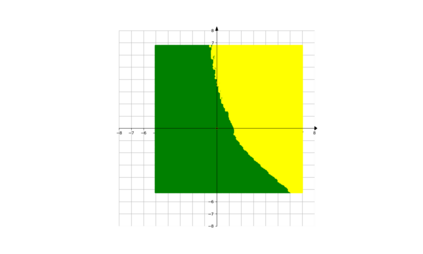
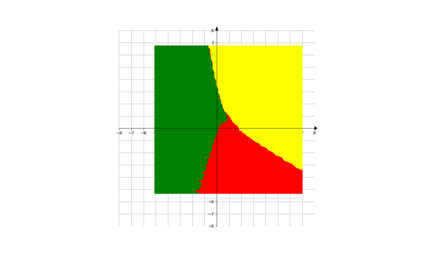
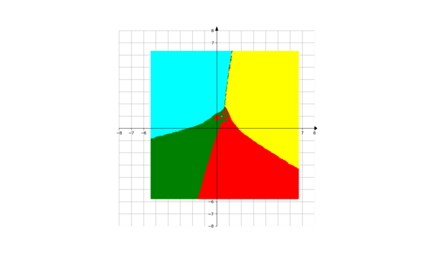
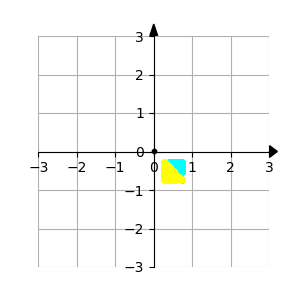
In root finding and optimization, there are many cases where there is a closed set $A$ one does not the sequence constructed by one's favourite method will converge to A (here, we do not assume extra properties on $A$ such as being convex or connected). For example, if one wants to find roots, and one chooses initial points in the basin of attraction for 1 root $x^*$ (a fact which one may not know before hand), then one will always end up in that root. In this case, one would like to have a mechanism to avoid this point $z^*$ in the next runs of one's algorithm. In this paper, we propose a new method aiming to achieve this: we divide the cost function by an appropriate power of the distance function to $A$. This idea is inspired by how one would try to find all roots of a function in 1 variable. We first explain the heuristic for this method in the case where the minimum of the cost function is exactly 0, and then explain how to proceed if the minimum is non-zero (allowing both positive and negative values). The method is very suitable for iterative algorithms which have the descent property. We also propose, based on this, an algorithm to escape the basin of attraction of a component of positive dimension to reach another component. Along the way, we compare with main existing relevant methods in the current literature. We provide several examples to illustrate the usefulness of the new approach.