Augmented Lagrangian Method based adjoint space framework for sparse reconstruction of acoustic source with boundary measurements

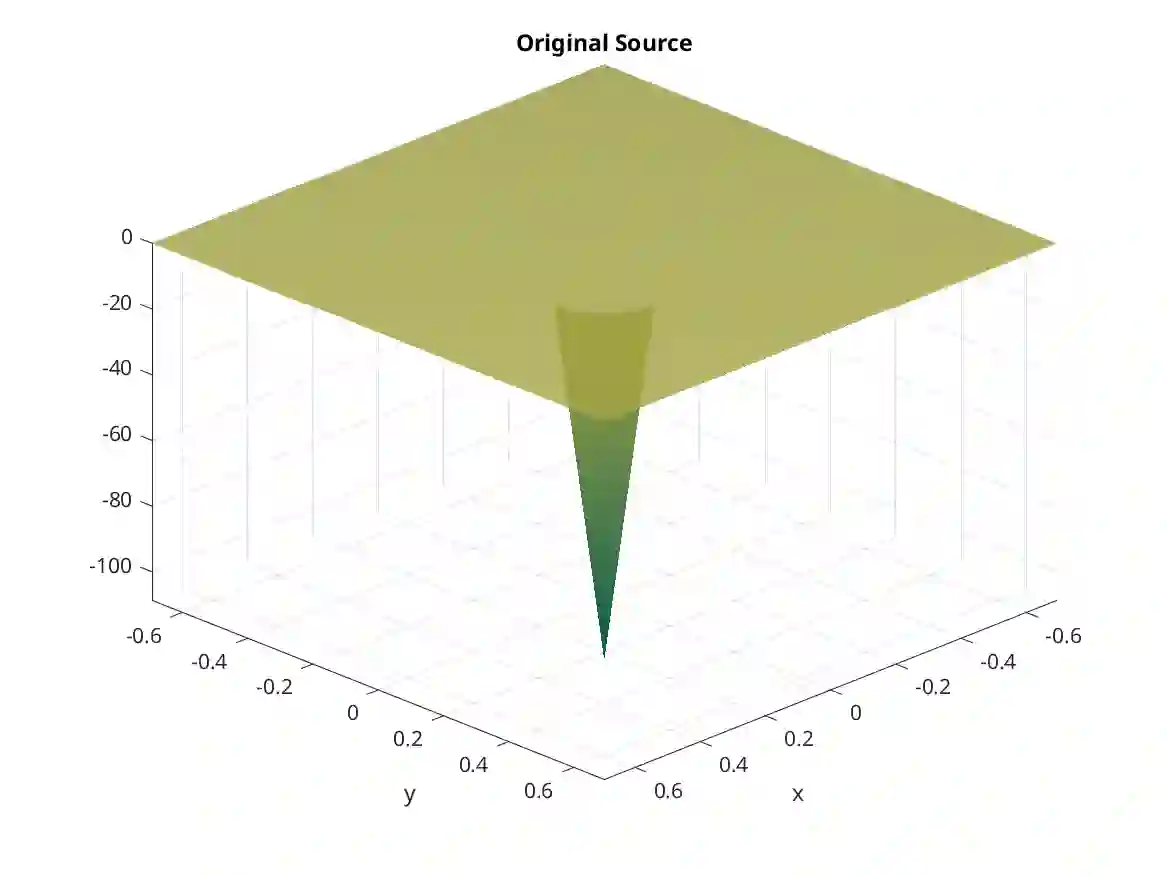
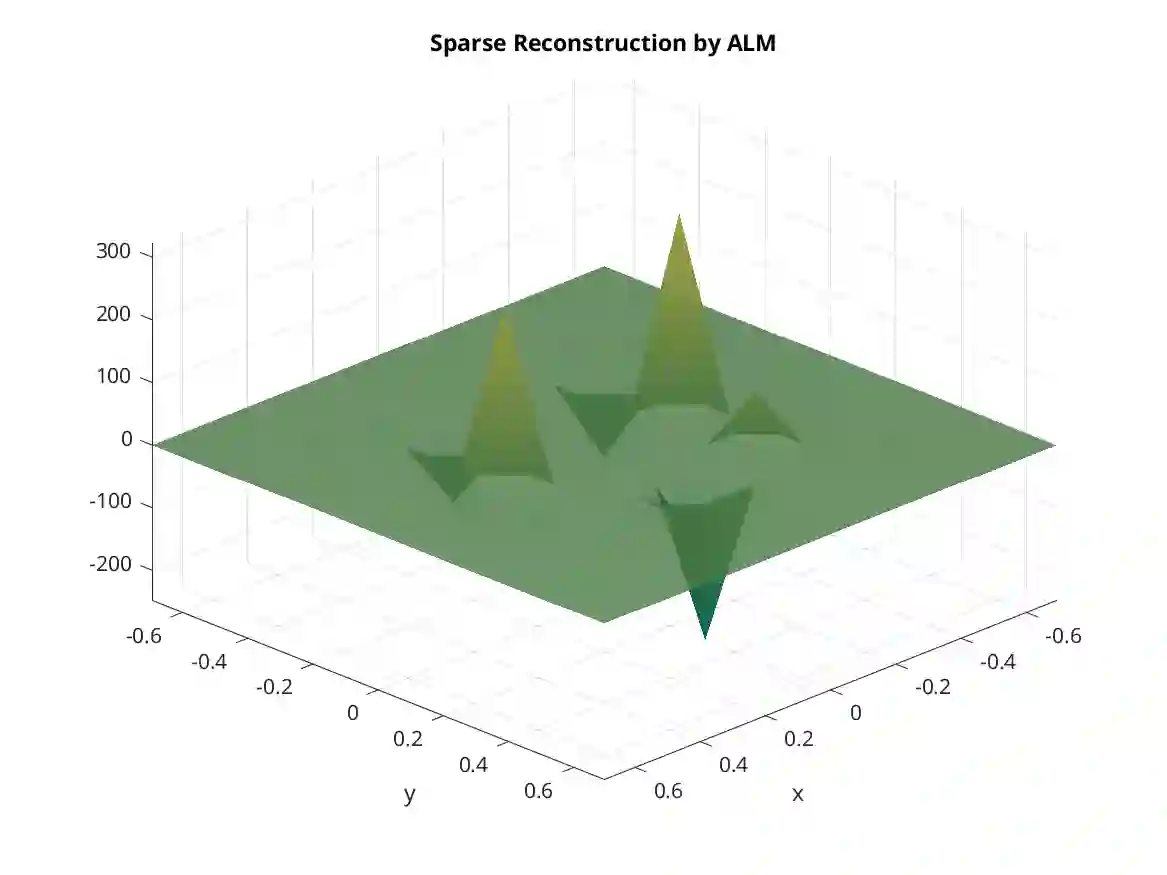
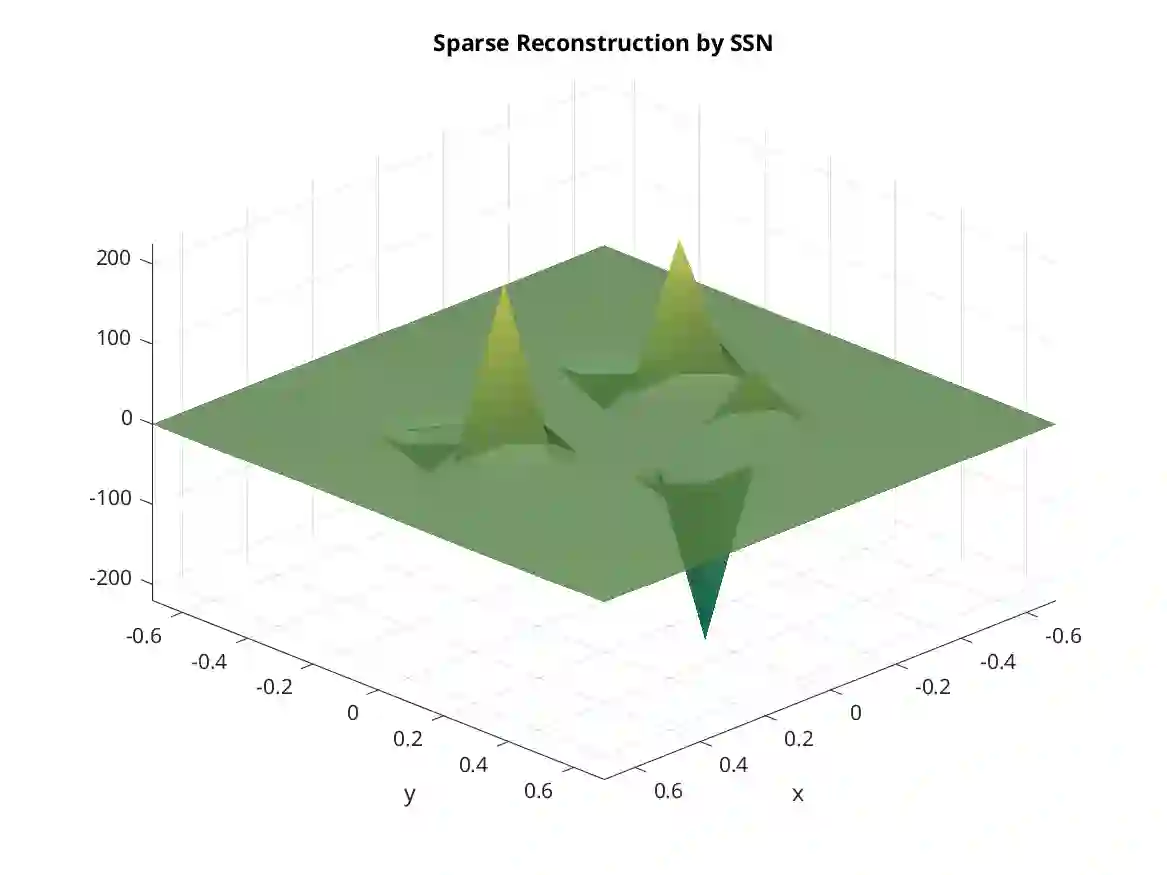
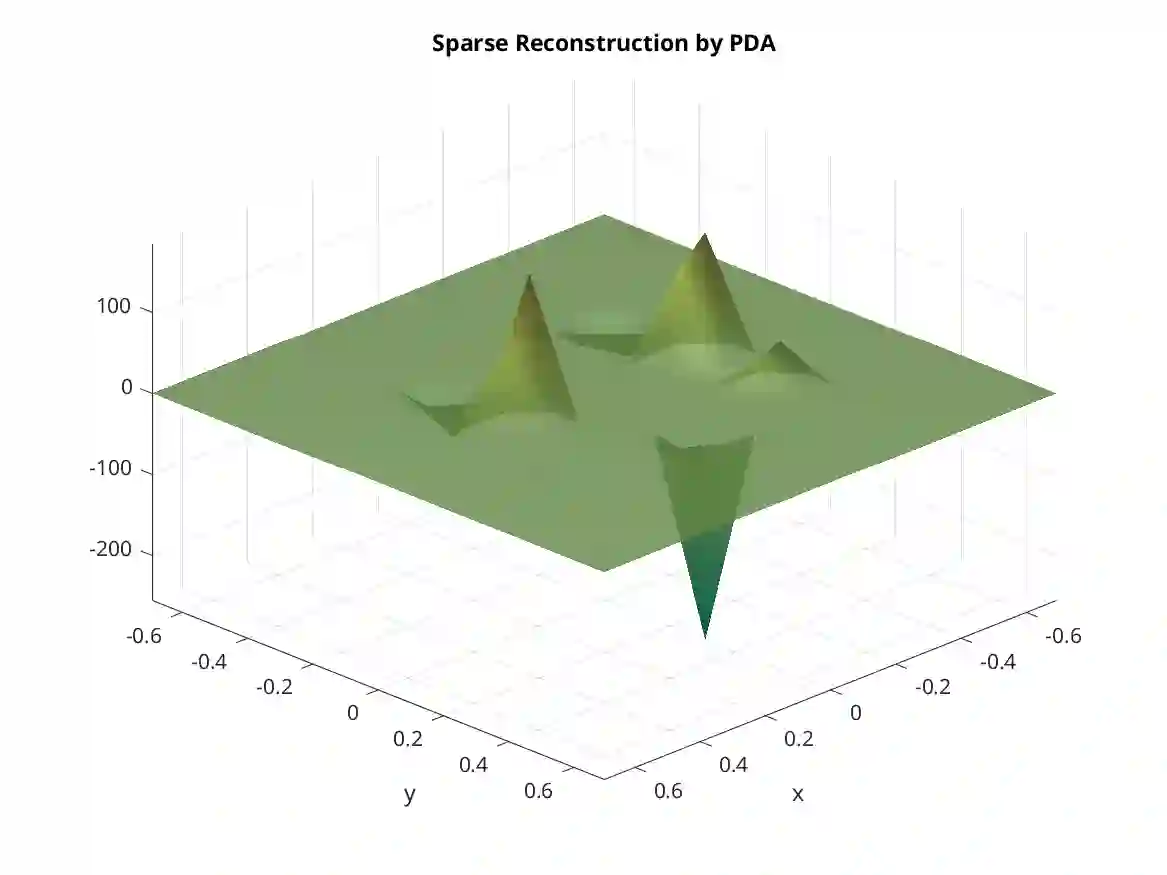
We propose a semismooth Newton-based augmented Lagrangian method for reconstructing sparse sources in inverse acoustic scattering problems. The semismooth Newton method can be iterated in the space of measurements instead of the unknown source to be reconstructed. It is highly efficient, especially when the measurement data is much less than the acoustic source. The source can be calculated from Fenchel-Rockafellar duality theory. We can obtain lots of acceleration and leverage the computational cost. The numerical examples show the high efficiency of the proposed semismooth Newton-based methods.