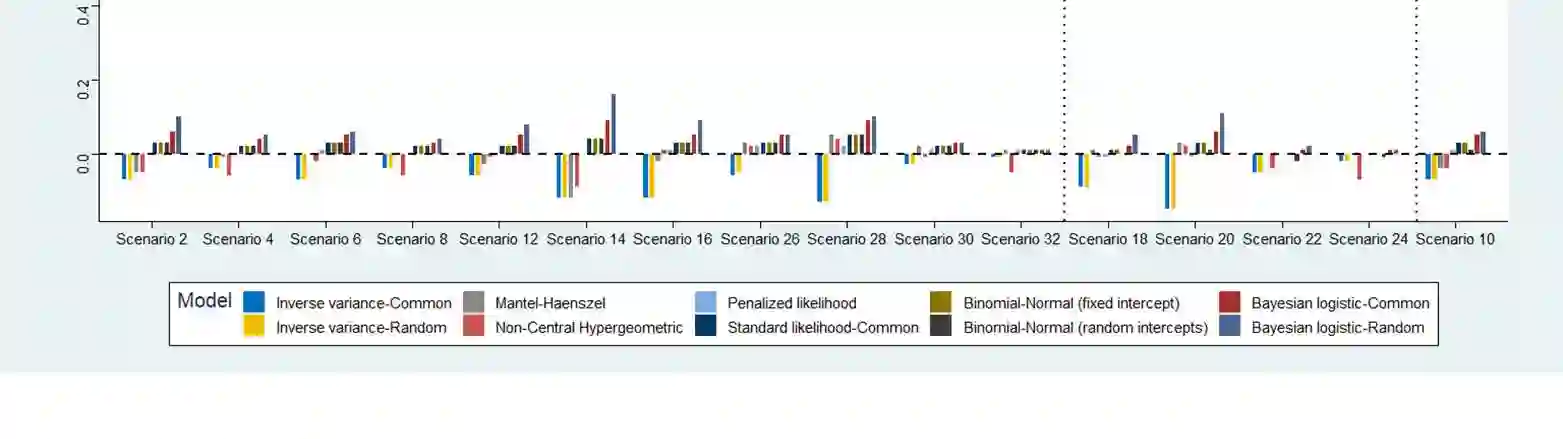
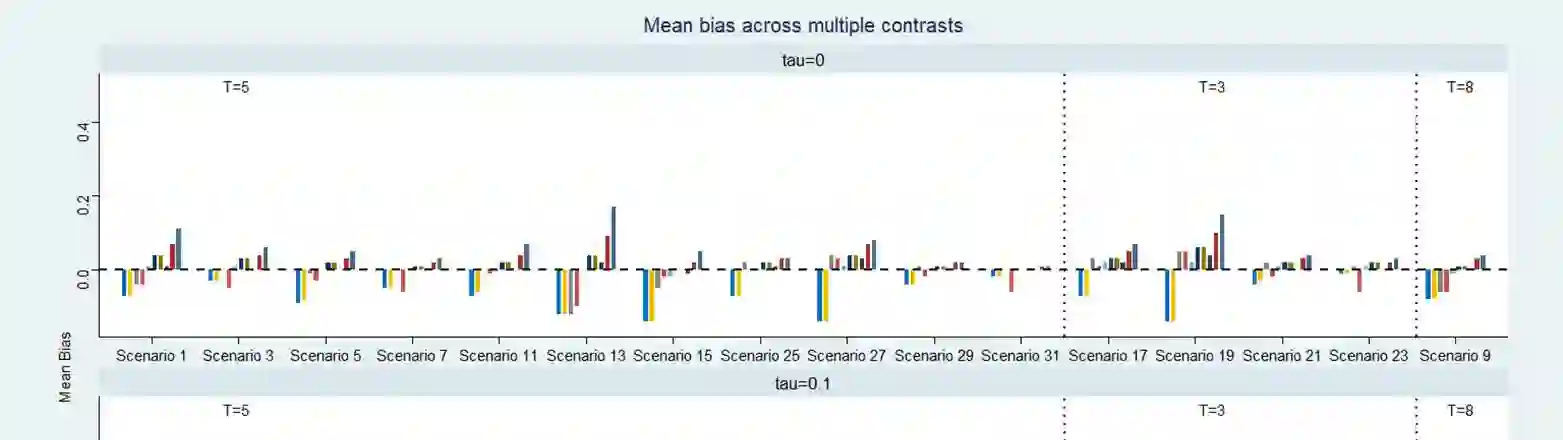
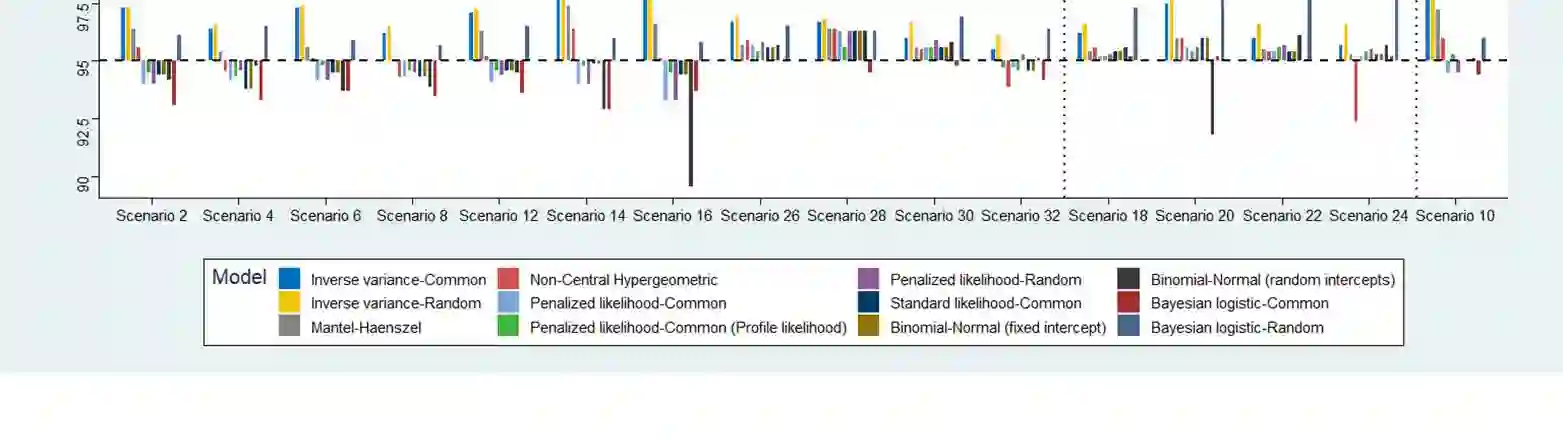
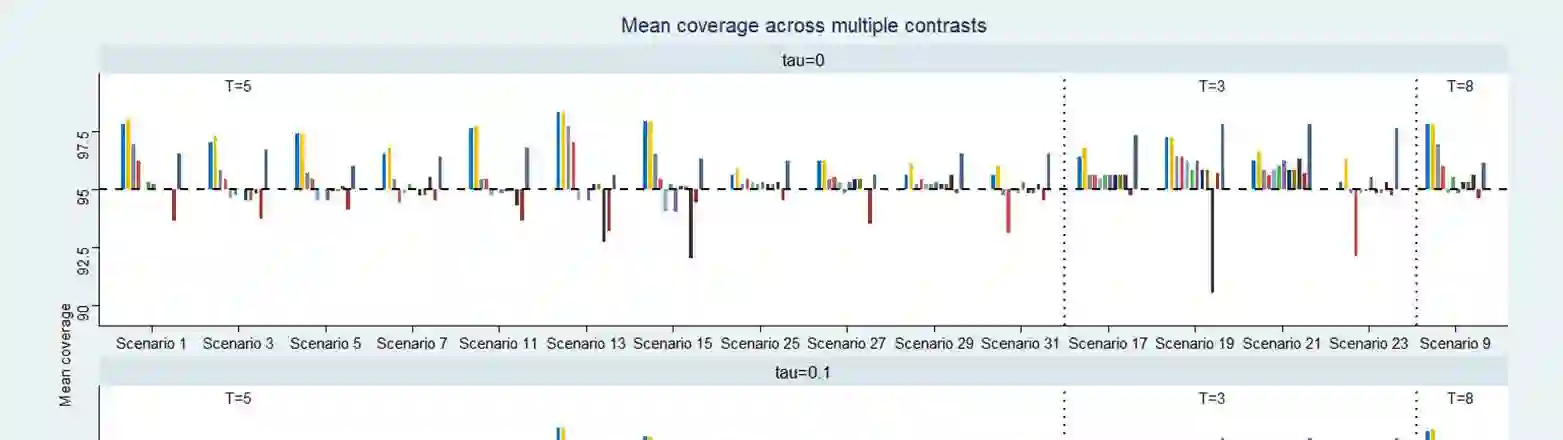
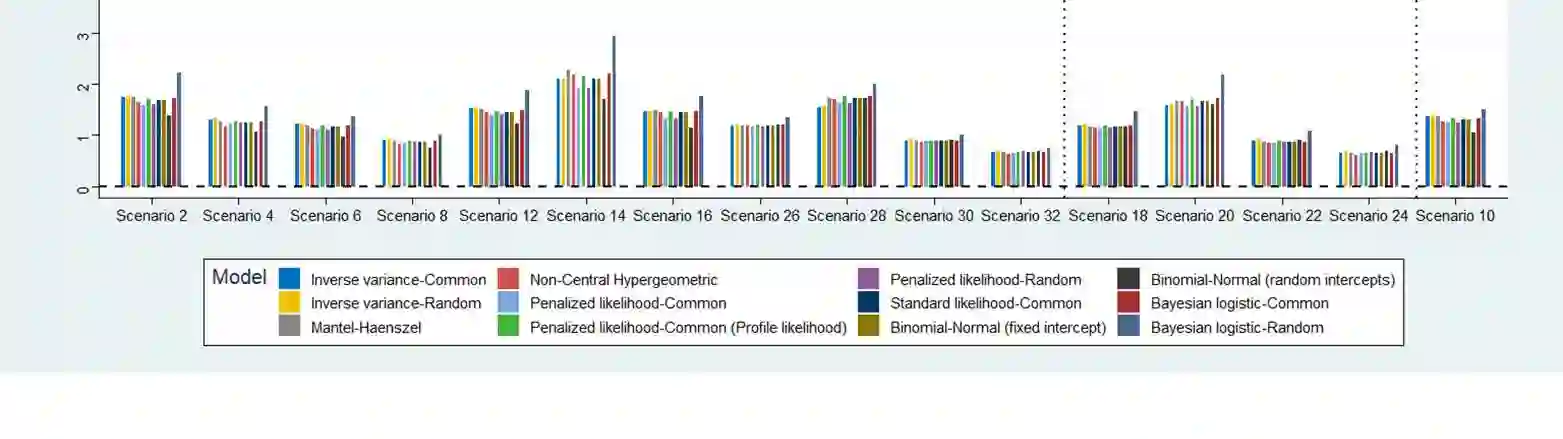
Network meta-analysis (NMA) of rare events has attracted little attention in the literature. Until recently, networks of interventions with rare events were analyzed using the inverse-variance NMA approach. However, when events are rare the normal approximation made by this model can be poor and effect estimates are potentially biased. Other methods for the synthesis of such data are the recent extension of the Mantel-Haenszel approach to NMA or the use of the non-central hypergeometric distribution. In this article, we suggest a new common-effect NMA approach that can be applied even in networks of interventions with extremely low or even zero number of events without requiring study exclusion or arbitrary imputations. Our method is based on the implementation of the penalized likelihood function proposed by Firth for bias reduction of the maximum likelihood estimate to the logistic expression of the NMA model. A limitation of our method is that heterogeneity cannot be taken into account as an additive parameter as in most meta-analytical models. However, we account for heterogeneity by incorporating a multiplicative overdispersion term using a two-stage approach. We show through simulations that our method performs consistently well across all tested scenarios and most often results in smaller bias than other available methods. We also illustrate the use of our method through two clinical examples. We conclude that our "penalized likelihood NMA" approach is promising for the analysis of binary outcomes with rare events especially for networks with very few studies per comparison and very low control group risks.
翻译:在文献中,对稀有事件的网络元分析(NMA)很少引起注意,直到最近,利用反向偏差NMA方法对稀有事件的干预网络进行了分析;然而,当情况少见时,该模型提出的正常近似值可能差,影响估计也可能有偏差;这类数据的其他综合方法包括最近将Mantel-Haenszel方法扩大到NMA,或使用非中央超地格分布法。在本篇文章中,我们建议采用一种新的共效NMA方法,即使在对极低或甚至零次于零的事件的干预网络中也可以应用,而不需要研究排斥或任意估计。我们的方法的基础是执行Firth提出的关于减少对NMA模型后勤表达的最大可能性估计的受罚可能性功能。我们的方法的一个局限性是,在多数元分析模型中,不能将异质性作为累加参数加以考虑。然而,我们通过使用两阶段方法的非常小的比较方法,我们经常通过模拟分析方法,用最可靠的方法来分析我们的所有原始分析结果。