Convergent regularization in inverse problems and linear plug-and-play denoisers

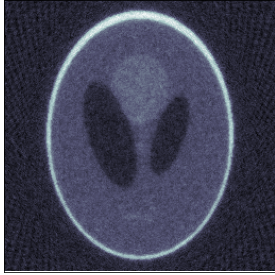
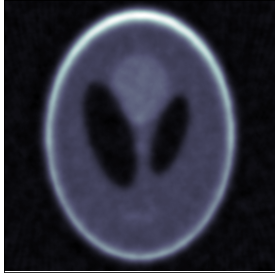
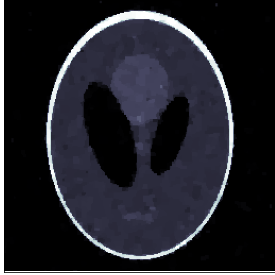
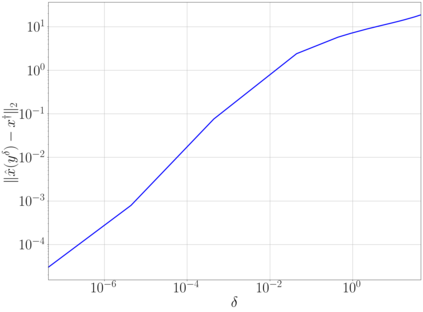
Plug-and-play (PnP) denoising is a popular iterative framework for solving imaging inverse problems using off-the-shelf image denoisers. Their empirical success has motivated a line of research that seeks to understand the convergence of PnP iterates under various assumptions on the denoiser. While a significant amount of research has gone into establishing the convergence of the PnP iteration for different regularity conditions on the denoisers, not much is known about the asymptotic properties of the converged solution as the noise level in the measurement tends to zero, i.e., whether PnP methods are provably convergent regularization schemes under reasonable assumptions on the denoiser. This paper serves two purposes: first, we provide an overview of the classical regularization theory in inverse problems and survey a few notable recent data-driven methods that are provably convergent regularization schemes. We then continue to discuss PnP algorithms and their established convergence guarantees. Subsequently, we consider PnP algorithms with linear denoisers and propose a novel spectral filtering technique to control the strength of regularization arising from the denoiser. Further, by relating the implicit regularization of the denoiser to an explicit regularization functional, we rigorously show that PnP with linear denoisers leads to a convergent regularization scheme. More specifically, we prove that in the limit as the noise vanishes, the PnP reconstruction converges to the minimizer of a regularization potential subject to the solution satisfying the noiseless operator equation. The theoretical analysis is corroborated by numerical experiments for the classical inverse problem of tomographic image reconstruction.