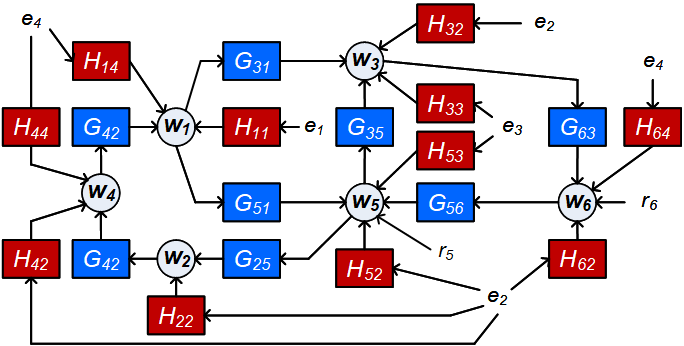
Identification methods for dynamic networks typically require prior knowledge of the network and disturbance topology, and often rely on solving poorly scalable non-convex optimization problems. While methods for estimating network topology are available in the literature, less attention has been paid to estimating the disturbance topology, i.e., the (spatial) noise correlation structure and the noise rank. In this work we present an identification method for dynamic networks, in which an estimation of the disturbance topology precedes the identification of the full dynamic network with known network topology. To this end we extend the multi-step Sequential Linear Regression and Weighted Null Space Fitting methods to deal with reduced rank noise, and use these methods to estimate the disturbance topology and the network dynamics. As a result, we provide a multi-step least squares algorithm with parallel computation capabilities and that rely only on explicit analytical solutions, thereby avoiding the usual non-convex optimizations involved. Consequently we consistently estimate dynamic networks of Box Jenkins model structure, while keeping the computational burden low. We provide a consistency proof that includes path-based data informativity conditions for allocation of excitation signals in the experimental design. Numerical simulations performed on a dynamic network with reduced rank noise clearly illustrate the potential of this method.
翻译:动态网络的识别方法通常需要事先了解网络和扰动地形学,并往往依靠解决不易缩放的非电解优化问题。文献中虽然有估算网络地形学的方法,但较少注意估计扰动地形学,即(空间)噪音相关结构以及噪音等级。在这项工作中,我们为动态网络提供了一种识别方法,其中对扰动地形学的估计先于查明已知网络地形学的完整动态网络。为此,我们扩大了多步线性线性递增和加权空格适应方法,以应对降级噪音,并使用这些方法估计扰动地形学和网络动态。结果,我们提供了具有平行计算能力的多步式最低方位算法,仅依赖于明确的分析解决办法,从而避免了通常的非电解优化。因此,我们始终不断地估算Box Jenkins模型结构的动态网络,同时保持较低的计算负担。我们提供了一致性证明,其中包括基于路径的数据,即用于配置动态网络的模拟,并清楚地说明在试验方法中进行的动态模拟。