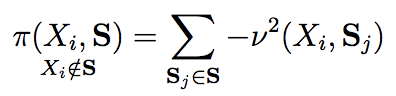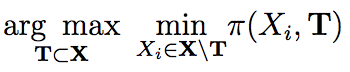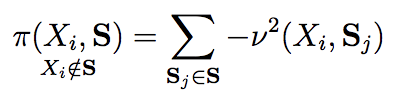Classes of set functions along with a choice of ground set are a bedrock to determine and develop corresponding variants of greedy algorithms to obtain efficient solutions for combinatorial optimization problems. The class of approximate constrained submodular optimization has seen huge advances at the intersection of good computational efficiency, versatility and approximation guarantees while exact solutions for unconstrained submodular optimization are NP-hard. What is an alternative to situations when submodularity does not hold? Can efficient and globally exact solutions be obtained? We introduce one such new frontier: The class of quasi-concave set functions induced as a dual class to monotone linkage functions. We provide a parallel algorithm with a time complexity over $n$ processors of $\mathcal{O}(n^2g) +\mathcal{O}(\log{\log{n}})$ where $n$ is the cardinality of the ground set and $g$ is the complexity to compute the monotone linkage function that induces a corresponding quasi-concave set function via a duality. The complexity reduces to $\mathcal{O}(gn\log(n))$ on $n^2$ processors and to $\mathcal{O}(gn)$ on $n^3$ processors. Our algorithm provides a globally optimal solution to a maxi-min problem as opposed to submodular optimization which is approximate. We show a potential for widespread applications via an example of diverse feature subset selection with exact global maxi-min guarantees upon showing that a statistical dependency measure called distance correlation can be used to induce a quasi-concave set function.
翻译:设定函数的分类, 加上对地面设置的选择, 是确定和开发相应的贪婪算法变种以获得组合优化问题的高效解决方案的基石 。 近似受限制亚模式优化类别在计算效率、 多功能性和近似保障的交叉点上取得了巨大进步, 而未限制亚模式优化的精确解决方案则是 NP- 硬。 美元是地面设置和美元问题的核心部分的替代方案是什么? 我们能否找到一个这样的新边框 : 类 类 类 类 准 concave 的贪婪算法, 以双级为单调连接功能。 我们提供一个具有时间复杂性的平行算法, 超过$\\ mathcal{O} (n\2g) QmallQQLiscal% Om) 。 美元是将单调的单调连接功能( eg- conve conve ) 函数通过双轨制, 导致相应的 类 准 conve conve 设置功能 。 级函数的复杂度降低到 $mathcal{ O_ lig lig lideal_ cal_ exal_ exal_ a procuilate a proclemental_ a proclementalmental_ a proclementalmental_ a procleglegleglemental) roclegleglemental_ a routtal_ a roglegleglegleglementaldroclemental