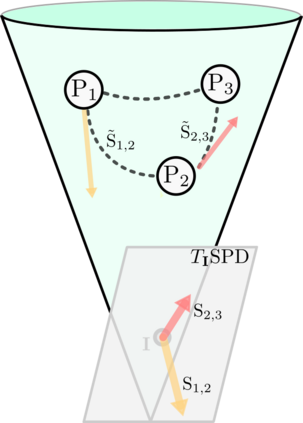
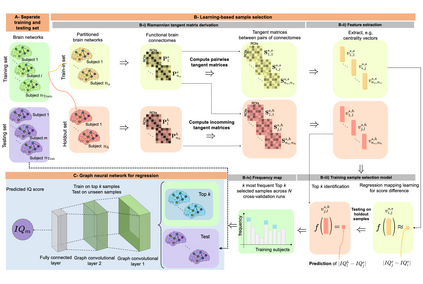
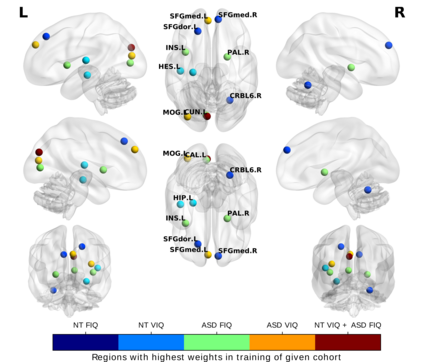
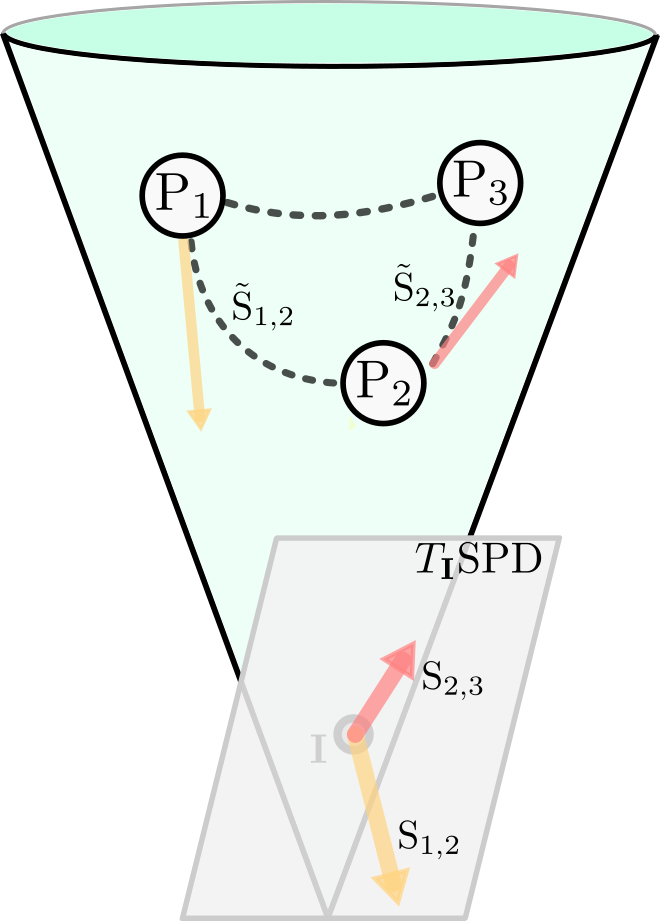
Analyzing the relation between intelligence and neural activity is of the utmost importance in understanding the working principles of the human brain in health and disease. In existing literature, functional brain connectomes have been used successfully to predict cognitive measures such as intelligence quotient (IQ) scores in both healthy and disordered cohorts using machine learning models. However, existing methods resort to flattening the brain connectome (i.e., graph) through vectorization which overlooks its topological properties. To address this limitation and inspired from the emerging graph neural networks (GNNs), we design a novel regression GNN model (namely RegGNN) for predicting IQ scores from brain connectivity. On top of that, we introduce a novel, fully modular sample selection method to select the best samples to learn from for our target prediction task. However, since such deep learning architectures are computationally expensive to train, we further propose a \emph{learning-based sample selection} method that learns how to choose the training samples with the highest expected predictive power on unseen samples. For this, we capitalize on the fact that connectomes (i.e., their adjacency matrices) lie in the symmetric positive definite (SPD) matrix cone. Our results on full-scale and verbal IQ prediction outperforms comparison methods in autism spectrum disorder cohorts and achieves a competitive performance for neurotypical subjects using 3-fold cross-validation. Furthermore, we show that our sample selection approach generalizes to other learning-based methods, which shows its usefulness beyond our GNN architecture.
翻译:分析智能和神经活动之间的关系对于理解人类大脑在健康和疾病方面的工作原理至关重要。在现有的文献中,功能性大脑连接体被成功地用于预测认知措施,如使用机器学习模型,健康组群和障碍组群的智能商数(IQ)分。然而,现有的方法采用通过忽略其地形特性的矢量化来平缓大脑连接体(即图),从而忽略其地形特性。为了应对这一局限性,并受新兴的图形神经网络(GNN)的启发,我们设计了一个新型的回归GNN模型(即RegGNN),用于预测大脑连通性IQ分数。此外,我们引入了一种新的、完全模块化的样本选择方法,选择最佳样本,以便从我们的目标预测任务中学习。然而,由于这种深层学习结构的计算成本非常昂贵,我们进一步建议一种基于 kemph{学习的样本选择方法。基于该方法学习如何选择具有最高预期的透析力。为此,我们利用连接性主体的GNNNNN模型(即RegGNNNNNNN)来预测大脑的智得分分分分分数。,我们用正式的模型显示正式的模型的模型的模型的正式模型显示正态结构。