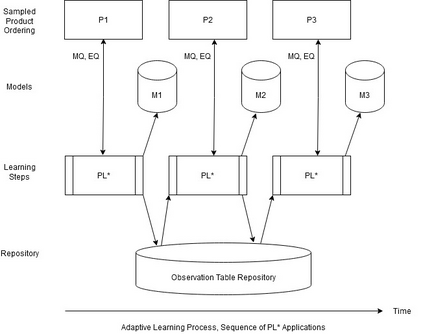
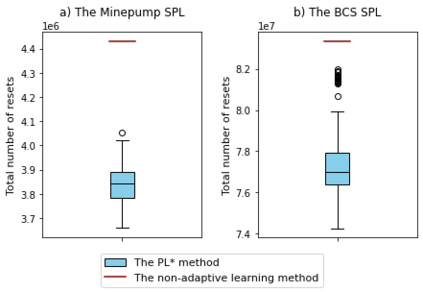
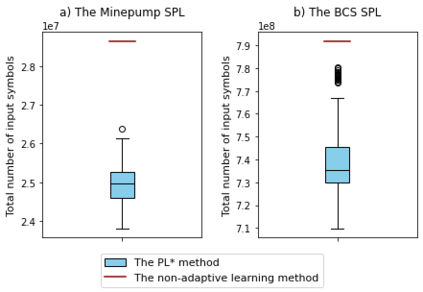
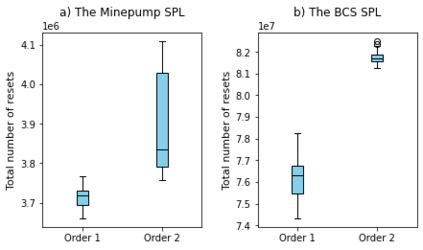
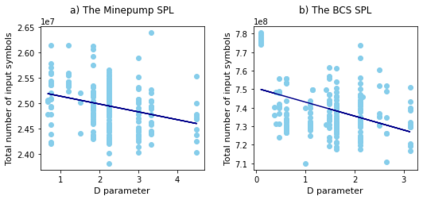
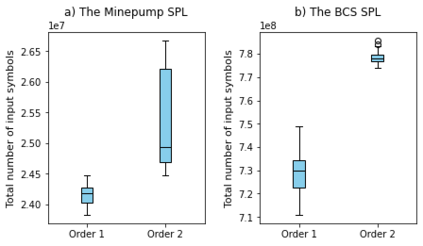
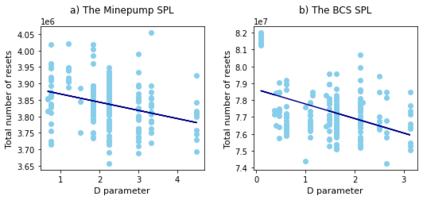
Behavioral models enable the analysis of the functionality of software product lines (SPL), e.g., model checking and model-based testing. Model learning aims at constructing behavioral models for software systems in some form of a finite state machine. Due to the commonalities among the products of an SPL, it is possible to reuse the previously learned models during the model learning process. In this paper, an adaptive approach (the $\text{PL}^*$ method) for learning the product models of an SPL is presented based on the well-known $L^*$ algorithm. In this method, after model learning of each product, the sequences in the final observation table are stored in a repository which will be used to initialize the observation table of the remaining products to be learned. The proposed algorithm is evaluated on two open-source SPLs and the total learning cost is measured in terms of the number of rounds, the total number of resets and input symbols. The results show that for complex SPLs, the total learning cost for the $\text{PL}^*$ method is significantly lower than that of the non-adaptive learning method in terms of all three metrics. Furthermore, it is observed that the order in which the products are learned affects the efficiency of the $\text{PL}^*$ method. Based on this observation, we introduced a heuristic to determine an ordering which reduces the total cost of adaptive learning in both case studies.
翻译:模型学习的目的是为软件系统以某种形式的有限状态机器的形式建立行为模型。由于SPL产品具有共同性,因此有可能在模型学习过程中重新使用以前学到的模型。在本文中,学习SPL产品模型的适应性方法($text{PL ⁇ $的方法)是根据众所周知的$L ⁇ $算法提出的。在这种方法中,在对每种产品进行模型学习后,最后观察表的序列将存储在一个存储库中,用于初始化有待学习的其余产品的观察表。拟议的算法将用两个开放源代码SPL产品加以评价,学习总成本将用圆轮数、Resetes和输入符号的总数来衡量。结果显示,对于复杂的SPLSL, $\pl{PL ⁇ $方法的总学习成本大大低于非适应性学习总成本,从所有三种观察方法的学习效率来看,这三种方法都降低了我们学习的学习水平。此外,在学习模型的排序中,我们观察到了三种方法的学习效率。