Helicity-conservative Physics-informed Neural Network Model for Navier-Stokes Equations

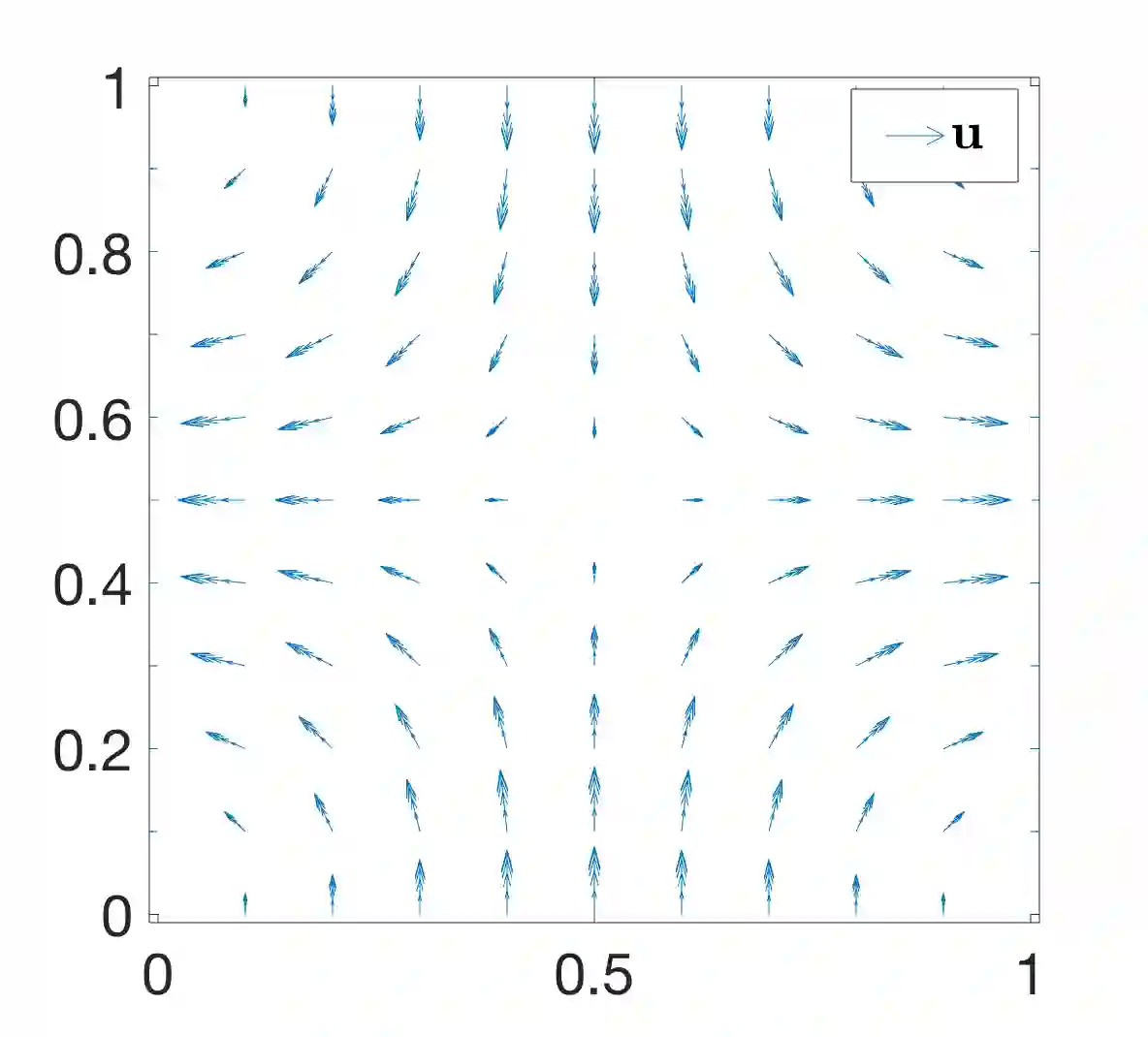
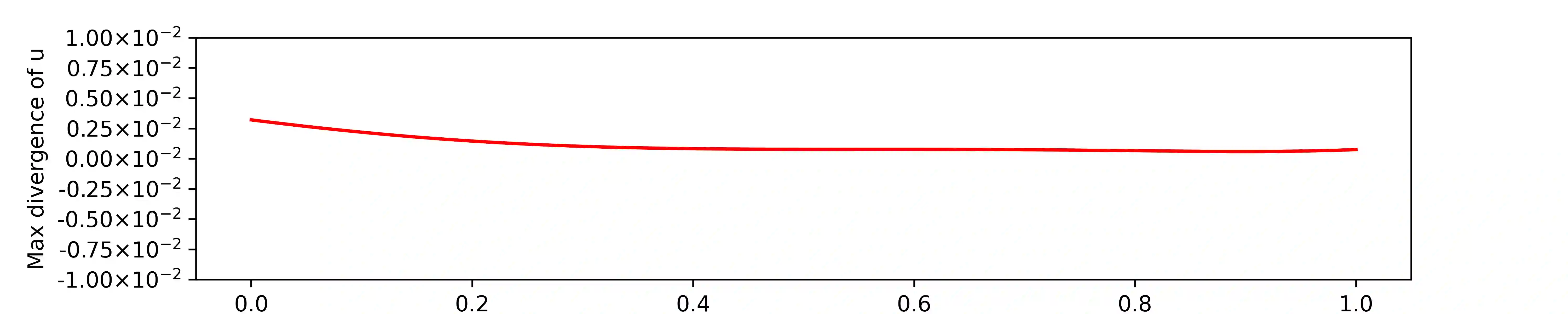
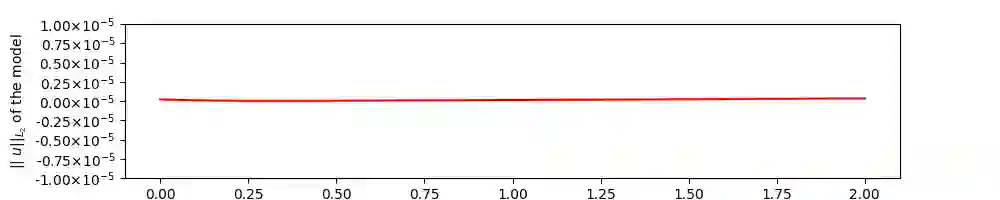
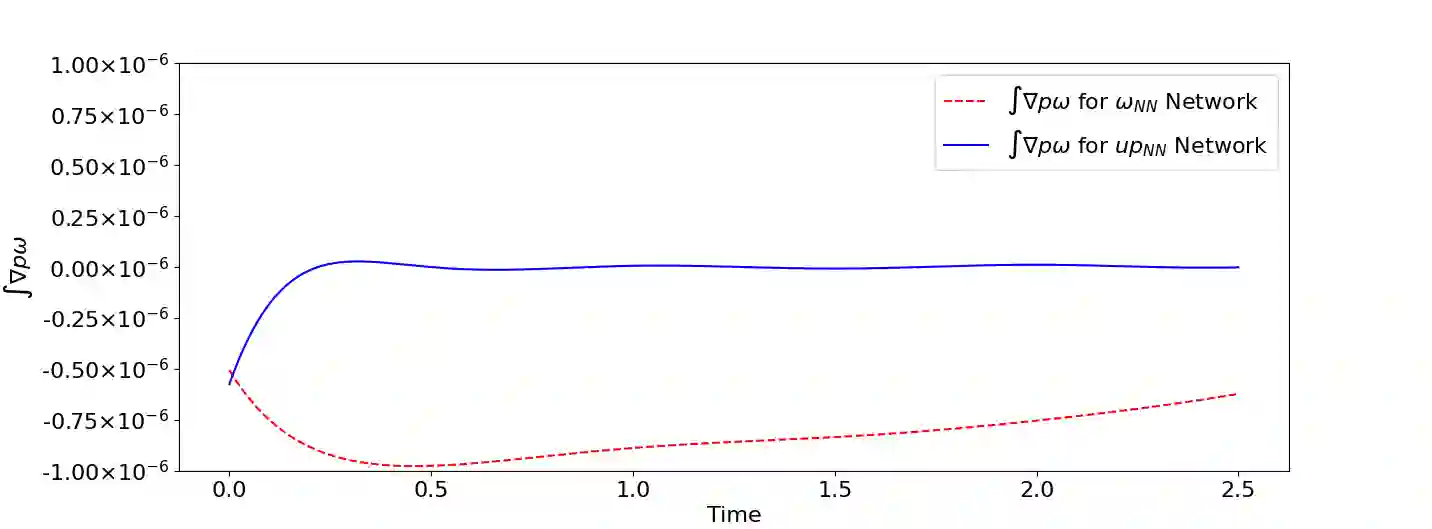
We design the helicity-conservative physics-informed neural network model for the Navier-Stokes equation in the ideal case. The key is to provide an appropriate PDE model as loss function so that its neural network solutions produce helicity conservation. Physics-informed neural network model is based on the strong form of PDE. We compare the proposed Physics-informed neural network model and a relevant helicity-conservative finite element method. We arrive at the conclusion that the strong form PDE is better suited for conservation issues. We also present theoretical justifications for helicity conservation as well as supporting numerical calculations.