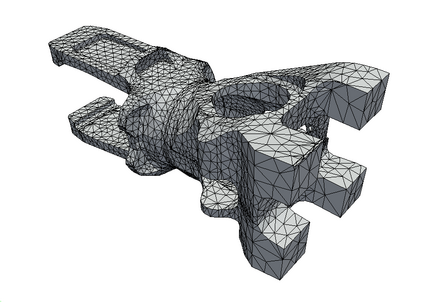
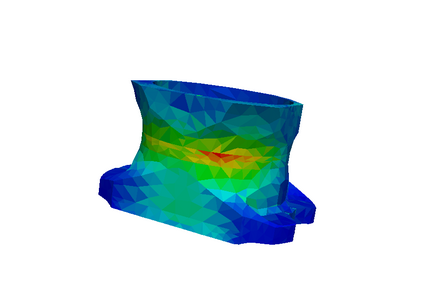
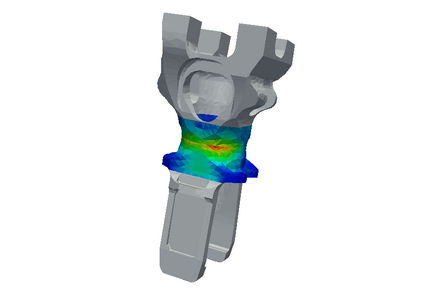
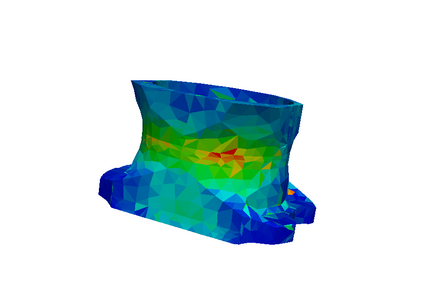
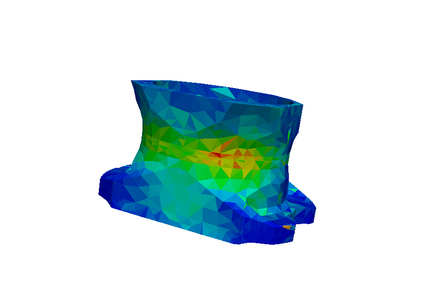
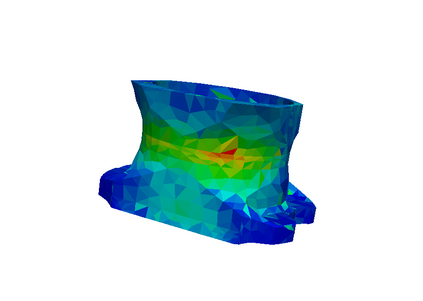
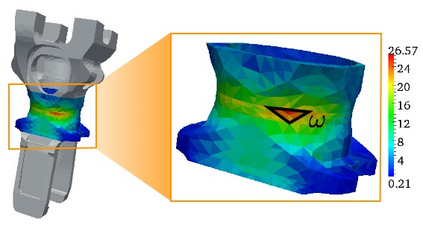
This article is a review on basic concepts and tools devoted to a posteriori error estimation for problems solved with the Finite Element Method. For the sake of simplicity and clarity, we mostly focus on linear elliptic diffusion problems, approximated by a conforming numerical discretization. The review mainly aims at presenting in a unified manner a large set of powerful verification methods, around the concept of equilibrium. Methods based on that concept provide error bounds that are fully computable and mathematically certified. We discuss recovery methods, residual methods, and duality-based methods for the estimation of the whole solution error (i.e. the error in energy norm), as well as goal-oriented error estimation (to assess the error on specific quantities of interest). We briefly survey the possible extensions to non-conforming numerical methods, as well as more complex (e.g. nonlinear or time-dependent) problems. We also provide some illustrating numerical examples on a linear elasticity problem in 3D.
翻译:本篇文章专门评述了用于对与有限元素法所解决问题进行事后误差估计的基本概念和工具。为了简单明晰,我们主要侧重于线性椭圆扩散问题,大致上采用一致数字分解法。审查的主要目的是围绕均衡概念统一提出一套强大的核查方法。基于这一概念的方法提供了完全可比较和数学认证的误差界限。我们讨论了用于估计整个解决方案错误(即能源规范中的错误)的回收方法、剩余方法和基于双重性的方法,以及着眼于目标的误差估计(评估特定利益量的误差)。我们简要考察了非对齐数字方法的可能扩展,以及更为复杂的问题(例如非线性或时间依赖性)。我们还提供了一些关于3D线性弹性问题的数字示例。