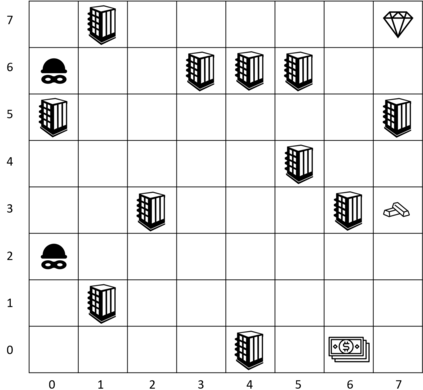
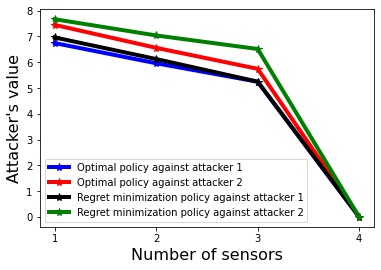
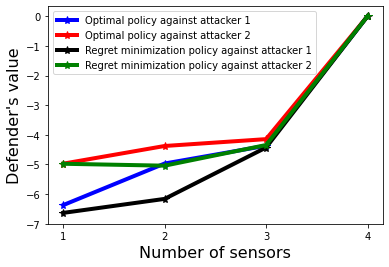
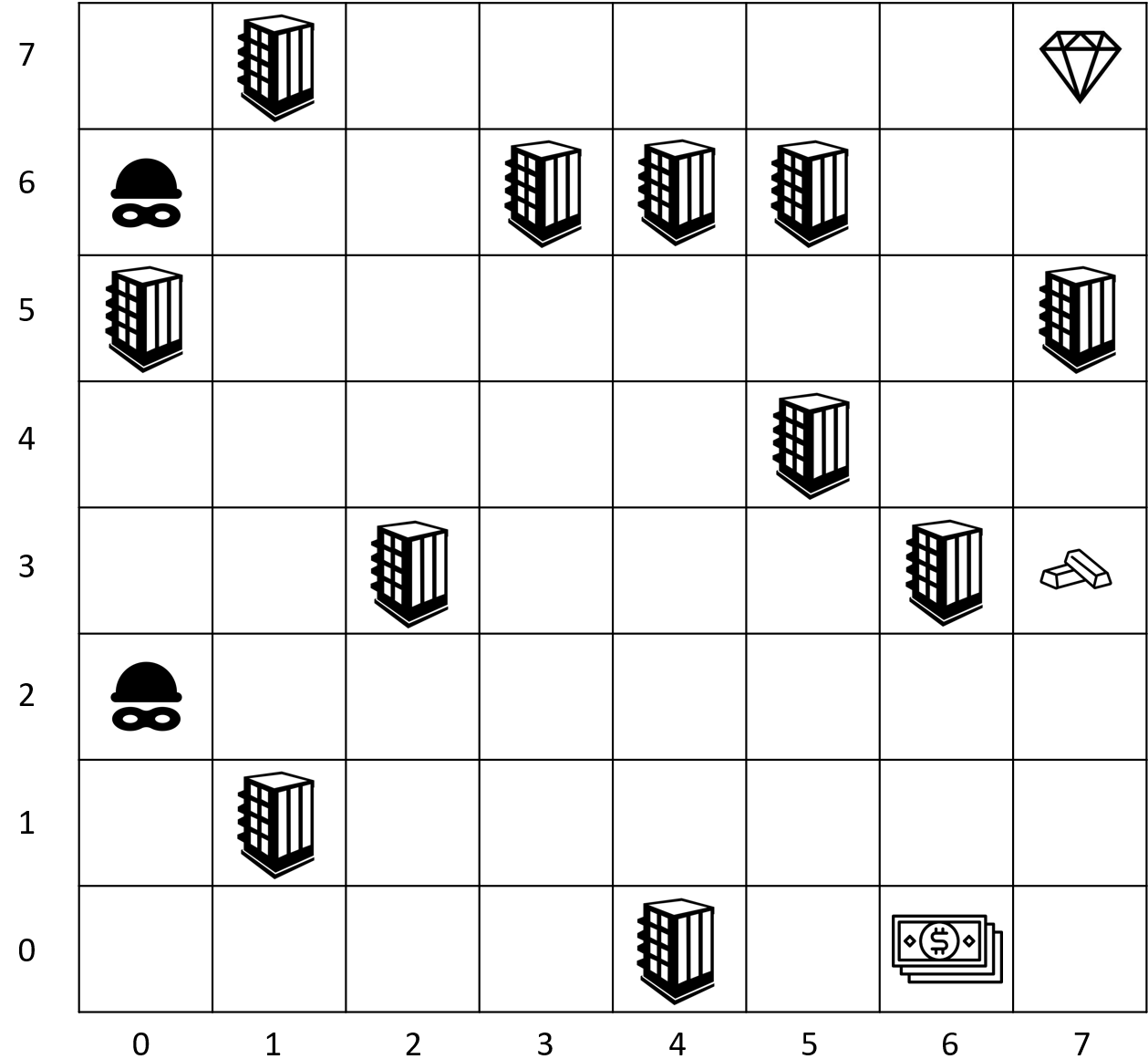
This paper is concerned with the optimal allocation of detection resources (sensors) to mitigate multi-stage attacks, in the presence of the defender's uncertainty in the attacker's intention. We model the attack planning problem using a Markov decision process and characterize the uncertainty in the attacker's intention using a finite set of reward functions -- each reward represents a type of the attacker. Based on this modeling framework, we employ the paradigm of the worst-case absolute regret minimization from robust game theory and develop mixed-integer linear program (MILP) formulations for solving the worst-case regret minimizing sensor allocation strategies for two classes of attack-defend interactions: one where the defender and attacker engage in a zero-sum game, and another where they engage in a non-zero-sum game. We demonstrate the effectiveness of our framework using a stochastic gridworld example.
翻译:本文关注于在防御者对攻击者意图存在不确定性的情况下,优化多阶段攻击的检测资源(传感器)分配。我们使用马尔可夫决策过程建模攻击计划问题,并使用一组有限的奖励函数来表征攻击者意图的不确定性,其中每个奖励函数都代表着一种攻击者类型。基于这个建模框架,我们采用鲁棒博弈论中的最坏情况绝对遗憾最小化范式,并制定混合整数线性规划(MILP)公式来求解零和博弈和非零和博弈两类攻防交互中的最坏情况遗憾最小化传感器分配策略。我们使用一个随机网格世界的例子来证明本文框架的有效性。