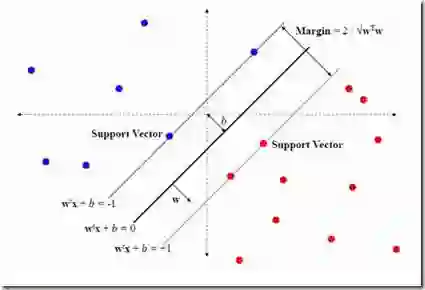
To model categorical response variables given their covariates, we propose a permuted and augmented stick-breaking (paSB) construction that one-to-one maps the observed categories to randomly permuted latent sticks. This new construction transforms multinomial regression into regression analysis of stick-specific binary random variables that are mutually independent given their covariate-dependent stick success probabilities, which are parameterized by the regression coefficients of their corresponding categories. The paSB construction allows transforming an arbitrary cross-entropy-loss binary classifier into a Bayesian multinomial one. Specifically, we parameterize the negative logarithms of the stick failure probabilities with a family of covariate-dependent softplus functions to construct nonparametric Bayesian multinomial softplus regression, and transform Bayesian support vector machine (SVM) into Bayesian multinomial SVM. These Bayesian multinomial regression models are not only capable of providing probability estimates, quantifying uncertainty, increasing robustness, and producing nonlinear classification decision boundaries, but also amenable to posterior simulation. Example results demonstrate their attractive properties and performance.
翻译:为了模拟具有共变性的绝对响应变量,我们建议采用一个固定且强化的刺破分解(pASB)构造,将观察到的类别一对一地绘制成随机随机地排列的潜潜伏棒。这个新的构造将多数值回归转换成对粘附特定二进随机变量的回归分析,这些变量是相互独立的,因为它们具有共变依赖的托盘成功概率,这些变量以相应类别中的回归系数为参数。这些巴伐利亚的多数值回归模型不仅能够提供概率估计,量化不确定性,增强稳健性,并产生非线性分类决定界限,而且还能向远古图像模拟显示其性能和性能。