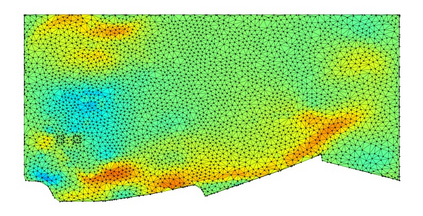
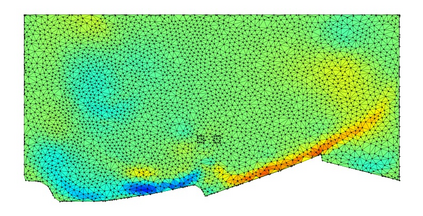
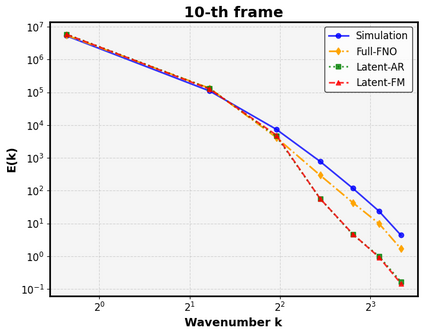
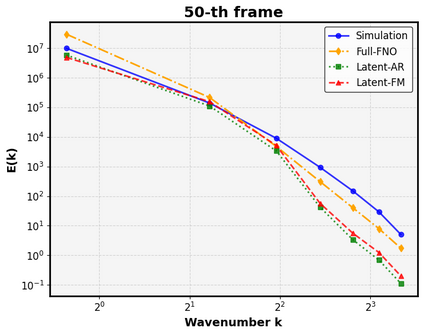
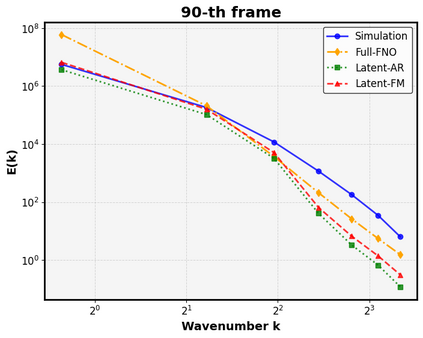
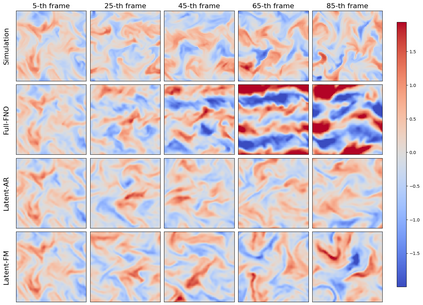
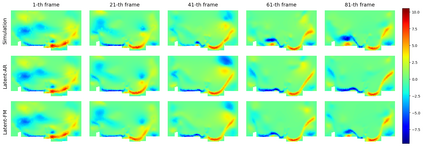
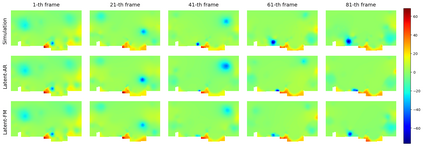
Autoregressive next-step prediction models have become the de-facto standard for building data-driven neural solvers to forecast time-dependent partial differential equations (PDEs). Denoise training that is closely related to diffusion probabilistic model has been shown to enhance the temporal stability of neural solvers, while its stochastic inference mechanism enables ensemble predictions and uncertainty quantification. In principle, such training involves sampling a series of discretized diffusion timesteps during both training and inference, inevitably increasing computational overhead. In addition, most diffusion models apply isotropic Gaussian noise on structured, uniform grids, limiting their adaptability to irregular domains. We propose a latent diffusion model for PDE simulation that embeds the PDE state in a lower-dimensional latent space, which significantly reduces computational costs. Our framework uses an autoencoder to map different types of meshes onto a unified structured latent grid, capturing complex geometries. By analyzing common diffusion paths, we propose to use a coarsely sampled noise schedule from flow matching for both training and testing. Numerical experiments show that the proposed model outperforms several deterministic baselines in both accuracy and long-term stability, highlighting the potential of diffusion-based approaches for robust data-driven PDE learning.
翻译:暂无翻译