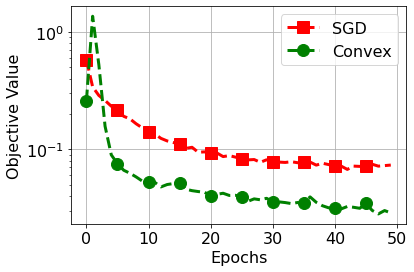
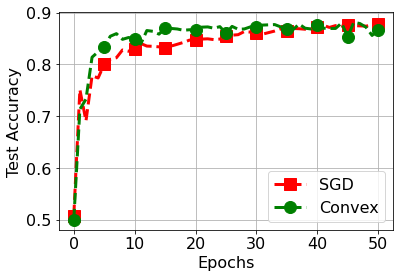
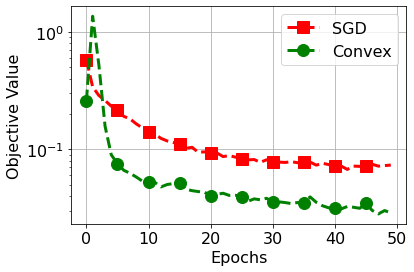
We study training of Convolutional Neural Networks (CNNs) with ReLU activations and introduce exact convex optimization formulations with a polynomial complexity with respect to the number of data samples, the number of neurons, and data dimension. More specifically, we develop a convex analytic framework utilizing semi-infinite duality to obtain equivalent convex optimization problems for several two- and three-layer CNN architectures. We first prove that two-layer CNNs can be globally optimized via an $\ell_2$ norm regularized convex program. We then show that multi-layer circular CNN training problems with a single ReLU layer are equivalent to an $\ell_1$ regularized convex program that encourages sparsity in the spectral domain. We also extend these results to three-layer CNNs with two ReLU layers. Furthermore, we present extensions of our approach to different pooling methods, which elucidates the implicit architectural bias as convex regularizers.
翻译:我们研究革命神经网络(CNNs)的ReLU激活,并引进精确的共振优化配方,在数据样本数量、神经元数量和数据维度方面具有多元复杂性。更具体地说,我们开发一个共振分析框架,利用半无穷的双重性,为多个两层和三层CNN架构获得等效的共振优化问题。我们首先证明,两层CNN可以通过一个$\ell_2美元规范的正规化convex程序在全球优化。我们然后显示,单层RELU多层的多层CNN培训问题相当于一个鼓励光谱域中宽度的多层CNN培训问题。我们还将这些结果推广到两个RU层次的三层CNN。此外,我们介绍了我们采用不同组合方法的延伸,该方法将隐含的建筑偏向作为Convex规范者加以解释。