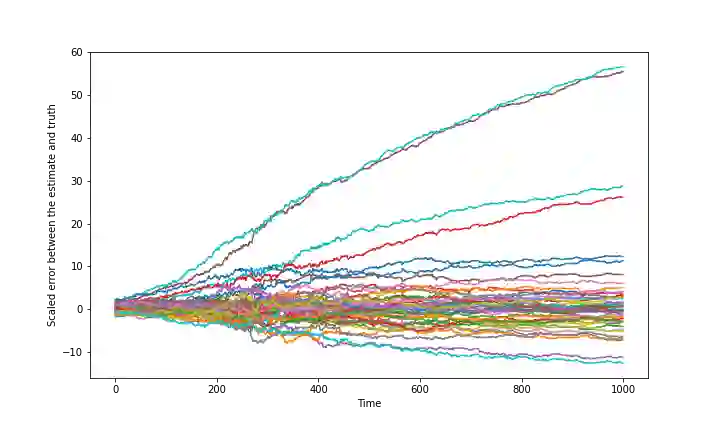
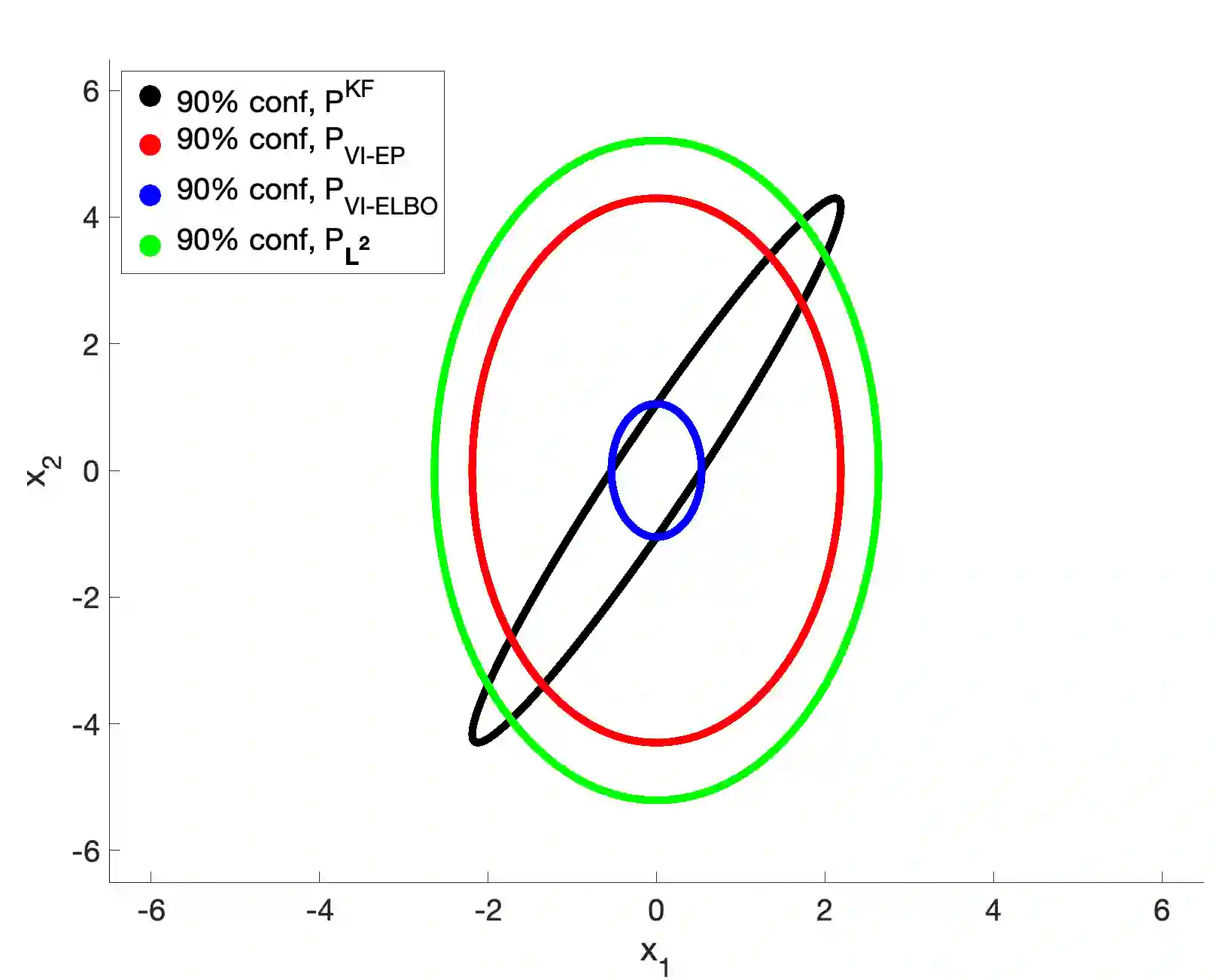
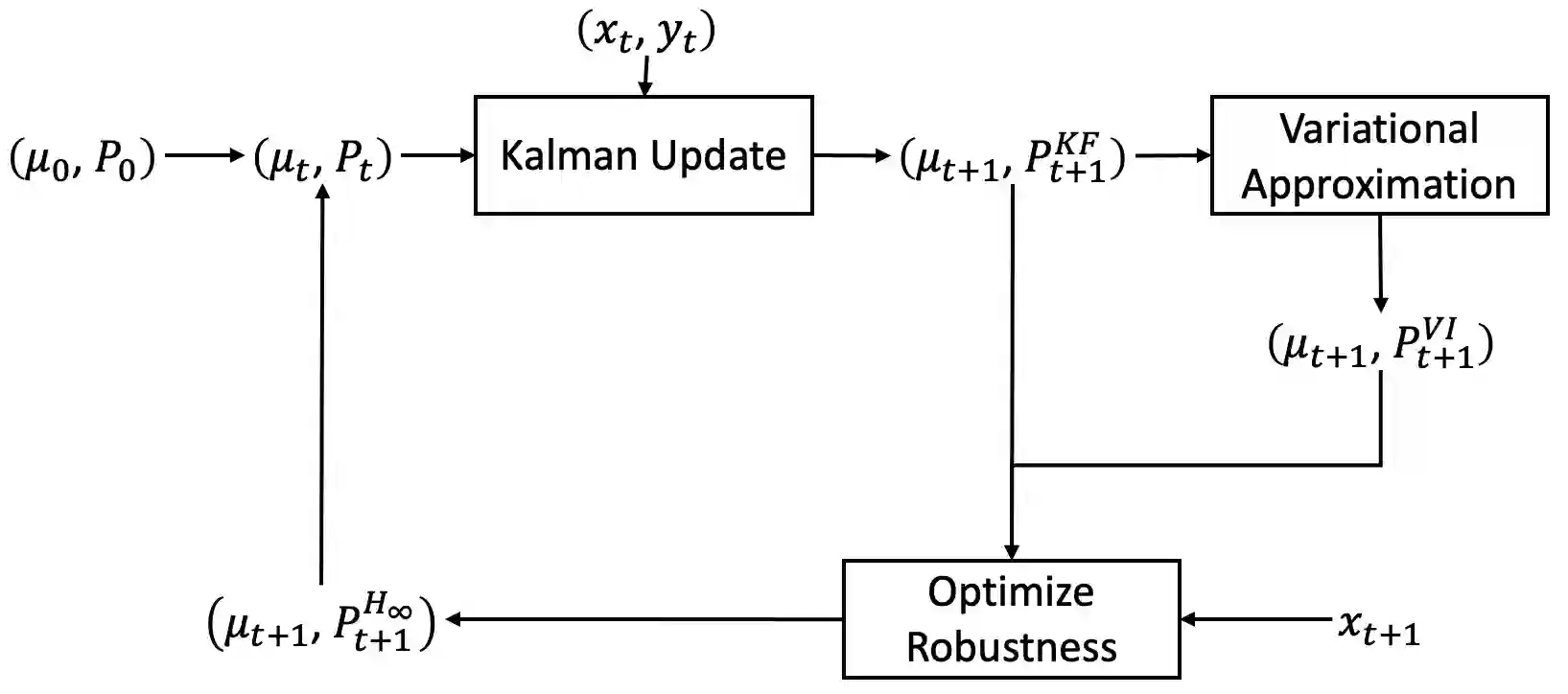
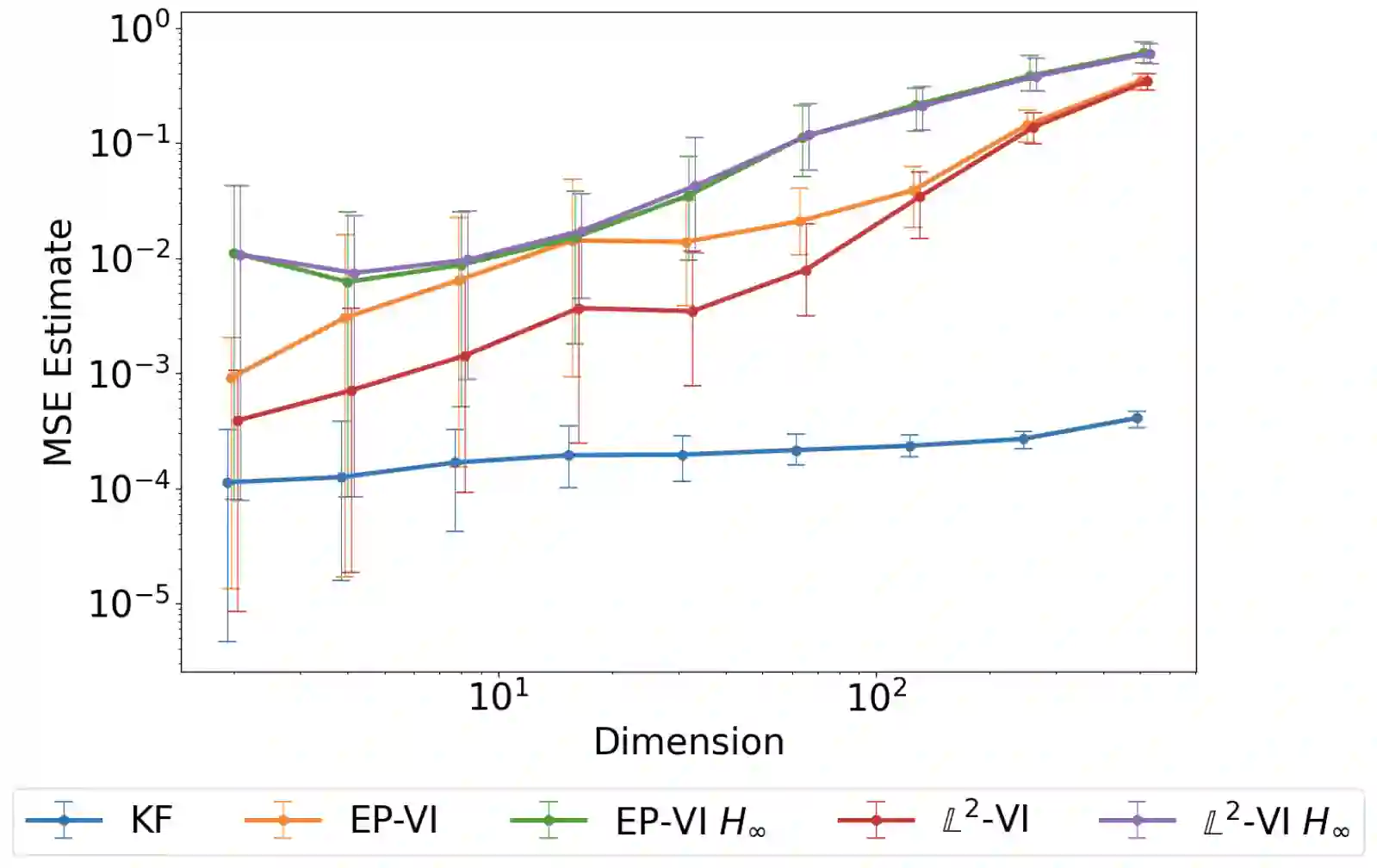
In this paper, we address the problem of convergence of sequential variational inference filter (VIF) through the application of a robust variational objective and Hinf-norm based correction for a linear Gaussian system. As the dimension of state or parameter space grows, performing the full Kalman update with the dense covariance matrix for a large scale system requires increased storage and computational complexity, making it impractical. The VIF approach, based on mean-field Gaussian variational inference, reduces this burden through the variational approximation to the covariance usually in the form of a diagonal covariance approximation. The challenge is to retain convergence and correct for biases introduced by the sequential VIF steps. We desire a framework that improves feasibility while still maintaining reasonable proximity to the optimal Kalman filter as data is assimilated. To accomplish this goal, a Hinf-norm based optimization perturbs the VIF covariance matrix to improve robustness. This yields a novel VIF- Hinf recursion that employs consecutive variational inference and Hinf based optimization steps. We explore the development of this method and investigate a numerical example to illustrate the effectiveness of the proposed filter.
翻译:在本文中,我们通过对直线高斯系统应用强大的变异目标和基于 Hinf-norm 的对线性高斯系统进行基于 Hinf-norm 的校正,解决顺序变异感过滤器(VIF ) 的趋同问题。随着状态或参数空间的维度增长,要用大型系统密集的共变式矩阵进行完整的卡尔曼更新,就需要增加储存和计算复杂性,使之不切实际。基于平均场高斯变异感应的VIF 方法,通过通常以对等变差近似形式出现的共变相近度减少这一负担。挑战是如何保持趋同,纠正依次的静态。我们希望有一个框架,既能提高可行性,同时又在数据同化时保持合理接近最佳的卡尔曼过滤器。要实现这一目标,基于 Hinf-norm 的优化就以VIF 变异性矩阵提高稳性。这产生了一个新的VIF-Hinf 重复性,利用连续的变异性和基于 Hinf 优化步骤。我们探索这一方法的发展,并研究一个数字示例。我们研究该方法的模型。