The structure and the list 3-dynamic coloring of outer-1-planar graphs

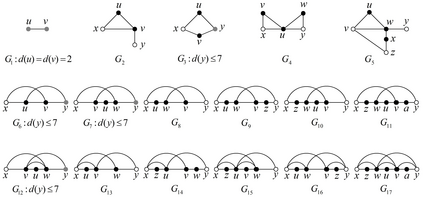
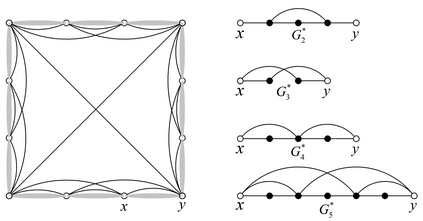
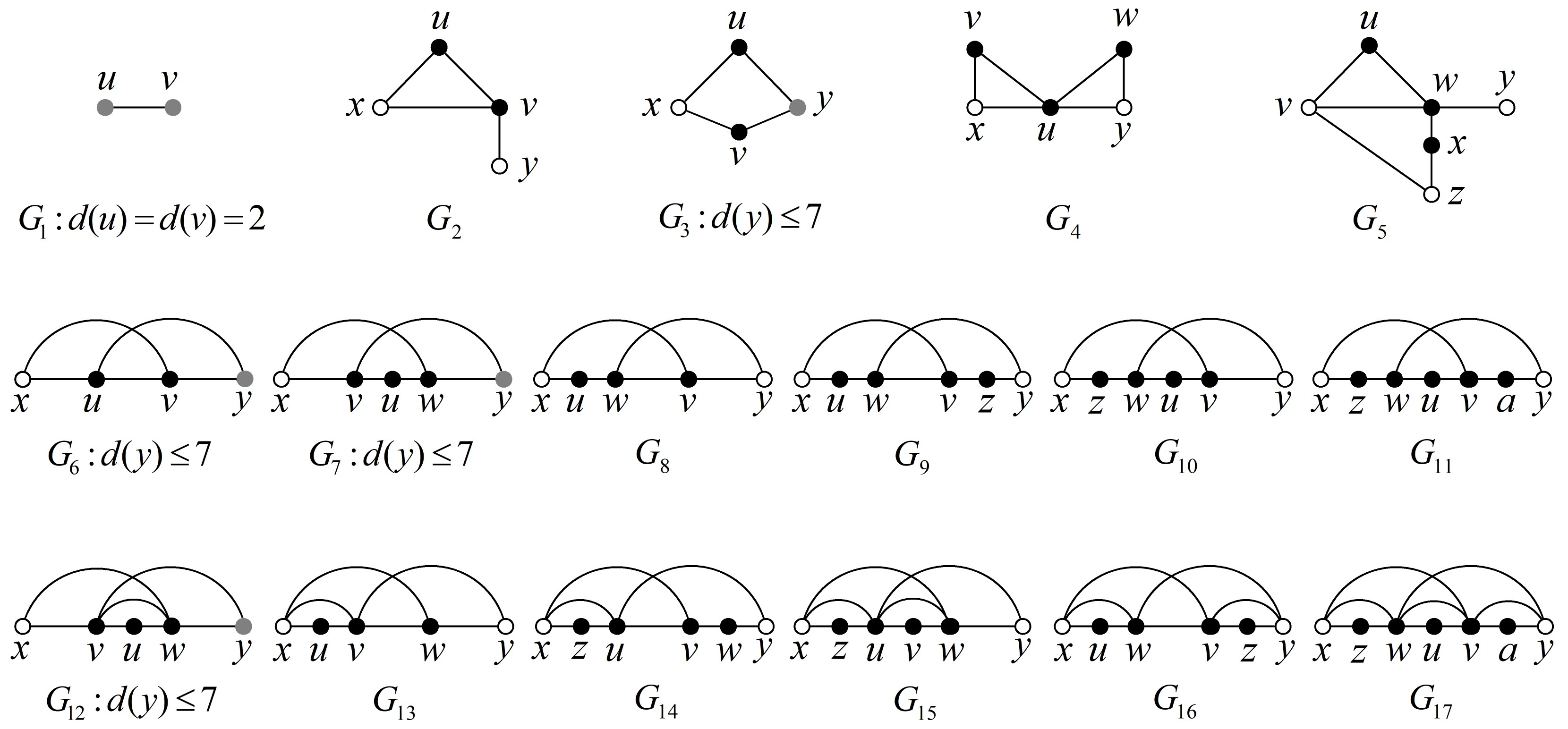
An outer-1-planar graph is a graph admitting a drawing in the plane so that all vertices appear in the outer region of the drawing and every edge crosses at most one other edge. This paper establishes the local structure of outer-1-planar graphs by proving that each outer-1-planar graph contains one of the seventeen fixed configurations, and the list of those configurations is minimal in the sense that for each fixed configuration there exist outer-1-planar graphs containing this configuration that do not contain any of another sixteen configurations. There are two interesting applications of this structural theorem. First of all, we conclude that every (resp.maximal) outer-1-planar graph of minimum degree at least 2 has an edge with the sum of the degrees of its two end-vertices being at most 9 (resp.7), and this upper bound is sharp. On the other hand, we show that the list 3-dynamic chromatic number of every outer-1-planar graph is at most 6, and this upper bound is best possible.