Decentralized Mean Field Games

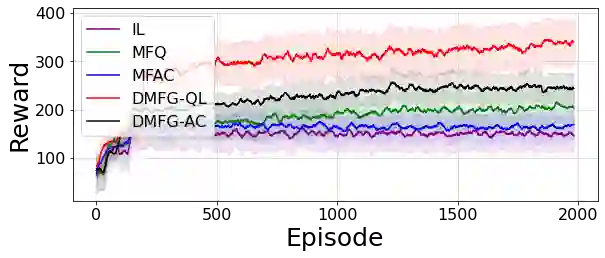
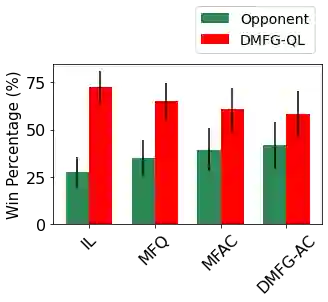
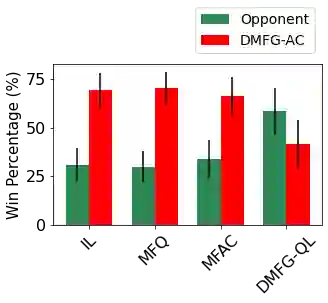
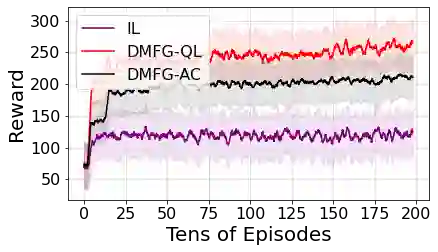
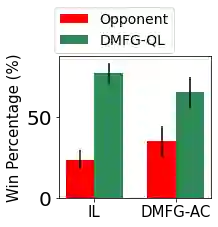
Multiagent reinforcement learning algorithms have not been widely adopted in large scale environments with many agents as they often scale poorly with the number of agents. Using mean field theory to aggregate agents has been proposed as a solution to this problem. However, almost all previous methods in this area make a strong assumption of a centralized system where all the agents in the environment learn the same policy and are effectively indistinguishable from each other. In this paper, we relax this assumption about indistinguishable agents and propose a new mean field system known as Decentralized Mean Field Games, where each agent can be quite different from others. All agents learn independent policies in a decentralized fashion, based on their local observations. We define a theoretical solution concept for this system and provide a fixed point guarantee for a Q-learning based algorithm in this system. A practical consequence of our approach is that we can address a `chicken-and-egg' problem in empirical mean field reinforcement learning algorithms. Further, we provide Q-learning and actor-critic algorithms that use the decentralized mean field learning approach and give stronger performances compared to common baselines in this area. In our setting, agents do not need to be clones of each other and learn in a fully decentralized fashion. Hence, for the first time, we show the application of mean field learning methods in fully competitive environments, large-scale continuous action space environments, and other environments with heterogeneous agents. Importantly, we also apply the mean field method in a ride-sharing problem using a real-world dataset. We propose a decentralized solution to this problem, which is more practical than existing centralized training methods.