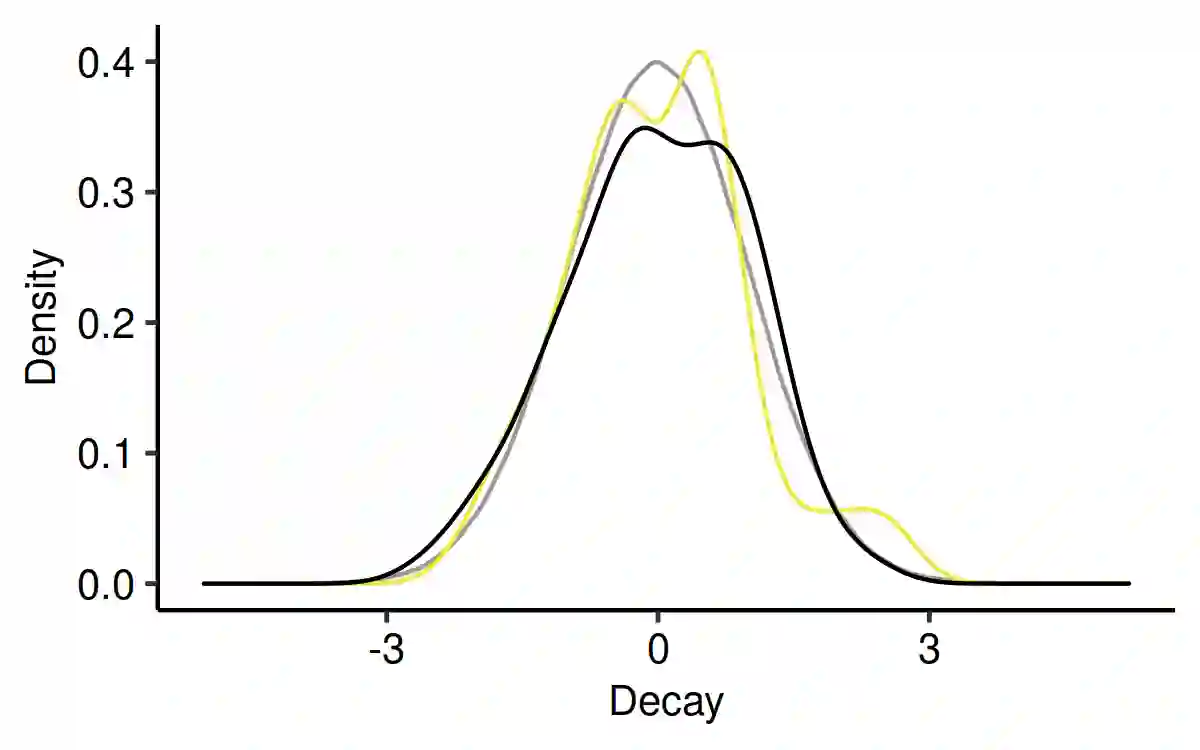
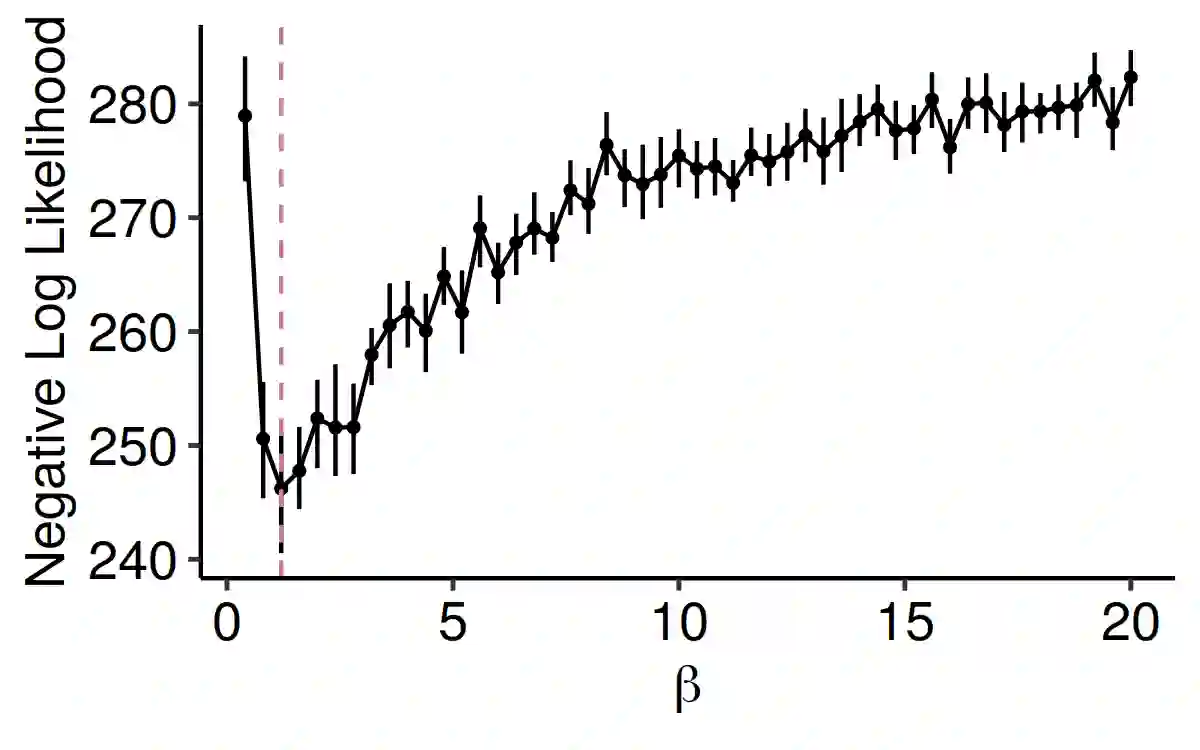
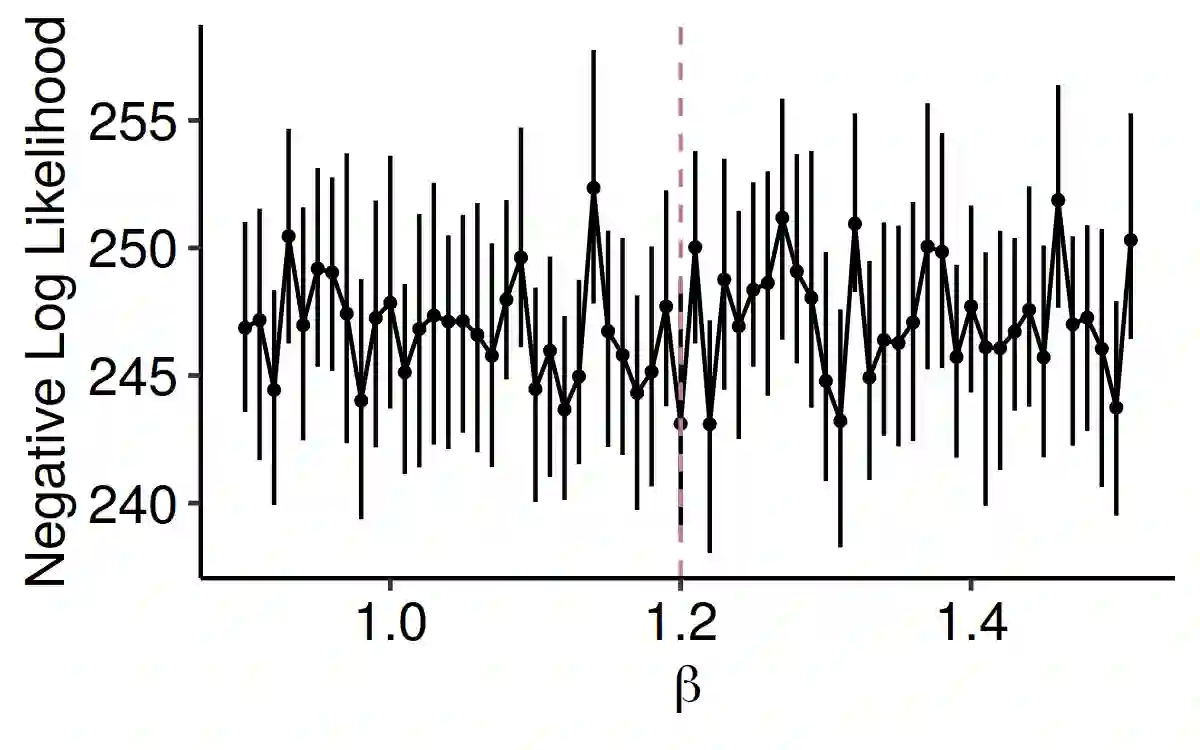
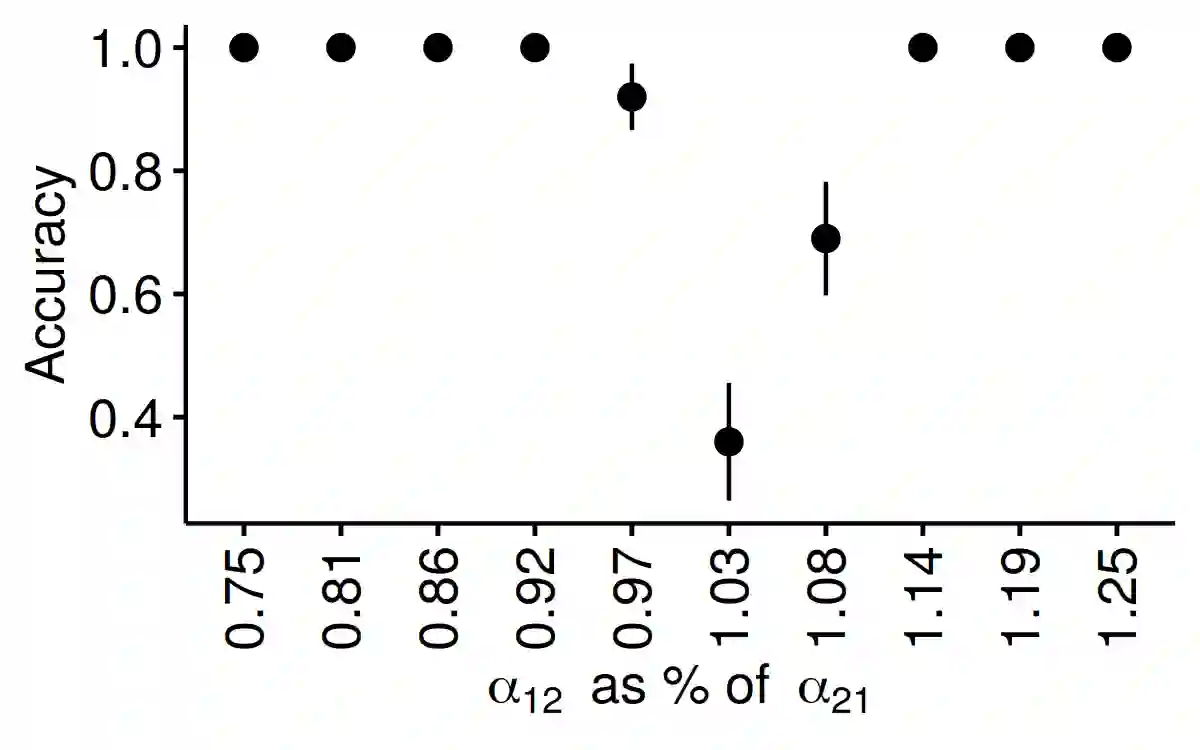
As a tool for capturing irregular temporal dependencies (rather than resorting to binning temporal observations to construct time series), Hawkes processes with exponential decay have seen widespread adoption across many application domains, such as predicting the occurrence time of the next earthquake or stock market spike. However, practical applications of Hawkes processes face a noteworthy challenge: There is substantial and often unquantified variance in decay parameter estimations, especially in the case of a small number of observations or when the dynamics behind the observed data suddenly change. We empirically study the cause of these practical challenges and we develop an approach to surface and thereby mitigate them. In particular, our inspections of the Hawkes process likelihood function uncover the properties of the uncertainty when fitting the decay parameter. We thus propose to explicitly capture this uncertainty within a Bayesian framework. With a series of experiments with synthetic and real-world data from domains such as "classical" earthquake modeling or the manifestation of collective emotions on Twitter, we demonstrate that our proposed approach helps to quantify uncertainty and thereby to understand and fit Hawkes processes in practice.
翻译:作为捕捉非正常时间依赖性的工具(而不是利用时间观测来构建时间序列),霍克斯进程在指数衰减过程中在许多应用领域被广泛采用,例如预测下一次地震发生时间或股票市场暴涨。然而,霍克斯进程的实际应用面临一个值得注意的挑战:在衰变参数估计方面,特别是在少数观测或观察到的数据的动态突然变化的情况下,在衰变参数估计方面,存在大量且往往没有量化的差异。我们实证地研究了这些实际挑战的原因,我们制定了表面挑战的方法,从而减轻了这些挑战。特别是,我们对霍克斯进程概率的检查发现,在符合衰变参数时,不确定性的特性会暴露出来。我们因此提议在拜耶斯框架内明确捕捉这种不确定性。我们用合成和现实世界数据进行了一系列实验,例如“古典”地震模型或推特上的集体情感表现,我们证明我们所提议的方法有助于量化不确定性,从而在实践中理解和适应霍克斯进程。