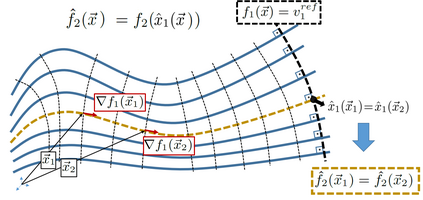
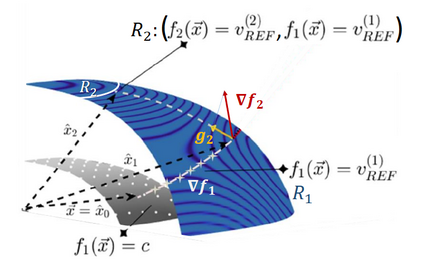
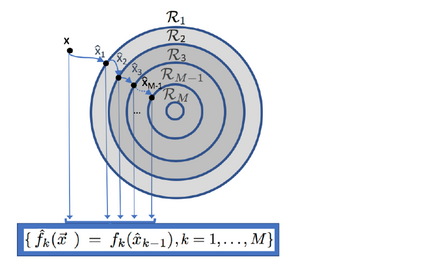
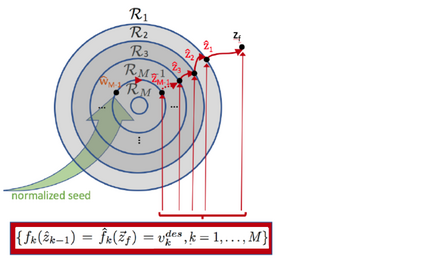
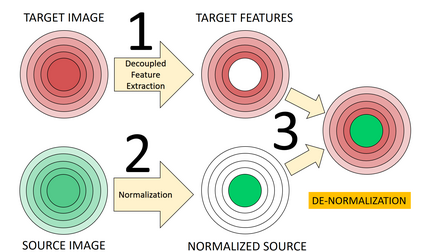
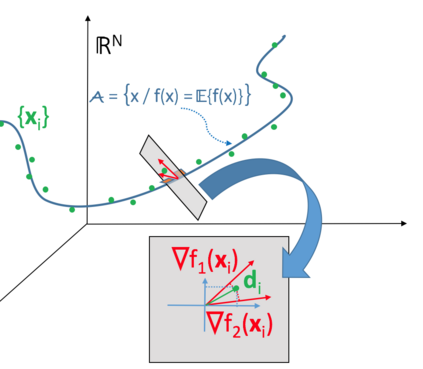
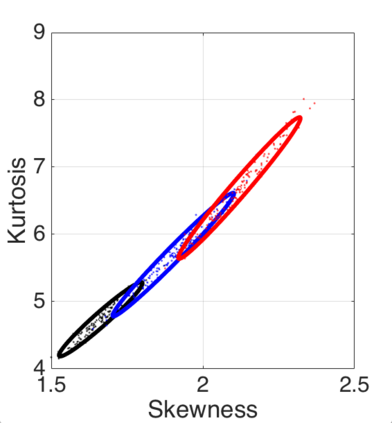
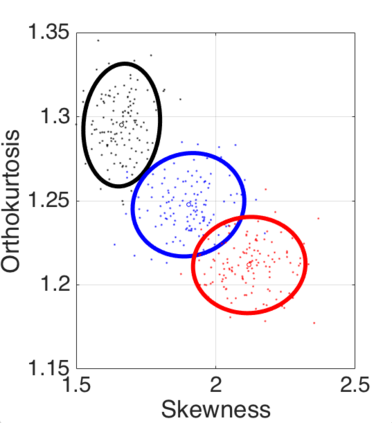
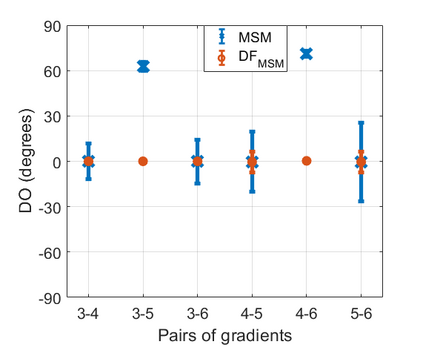
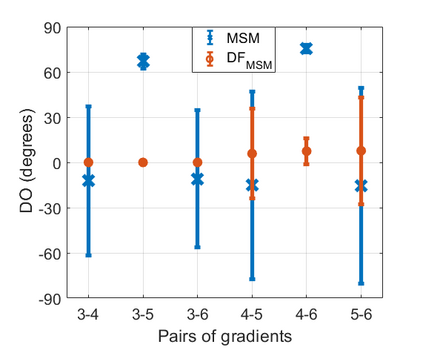
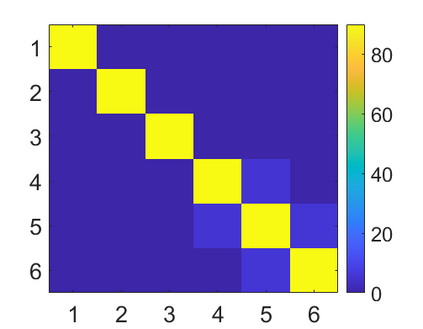
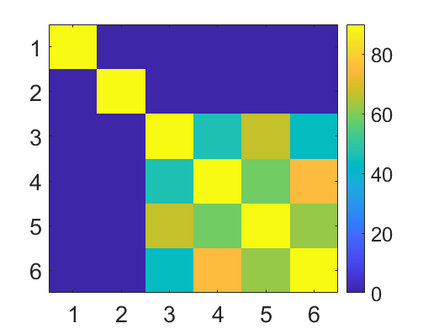
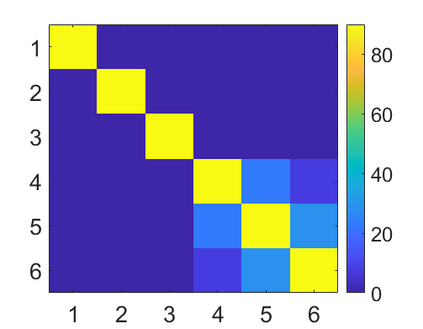
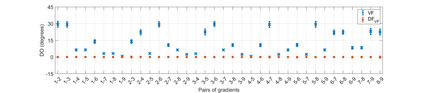
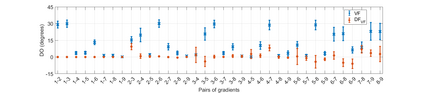
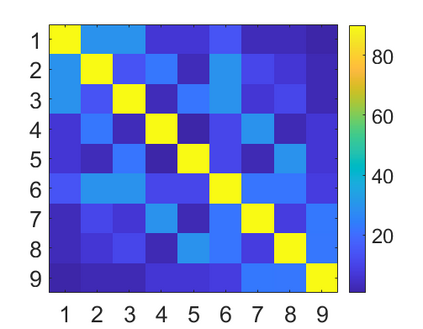
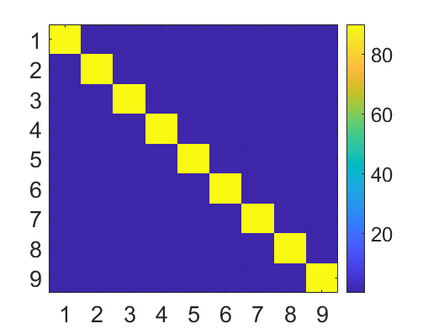
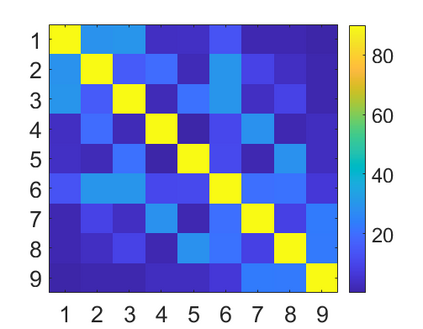
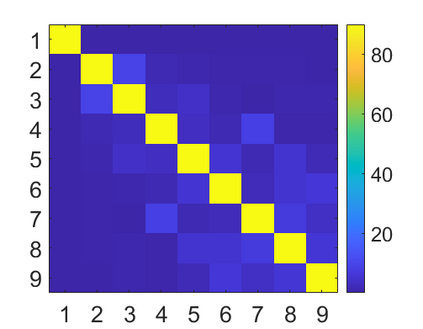
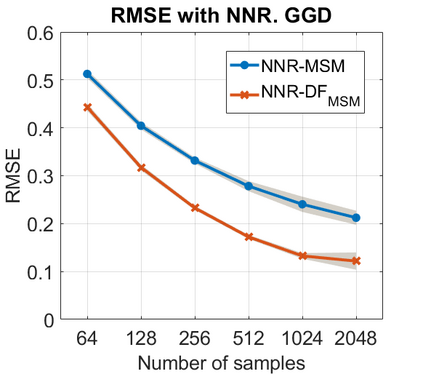
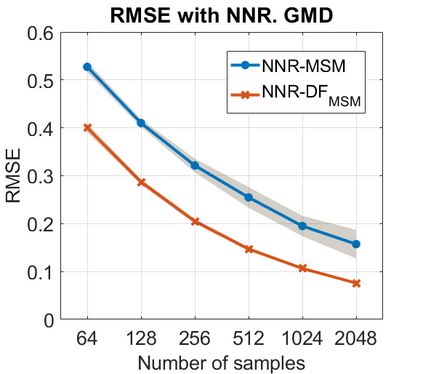
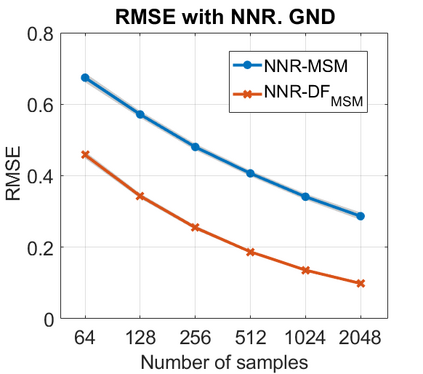
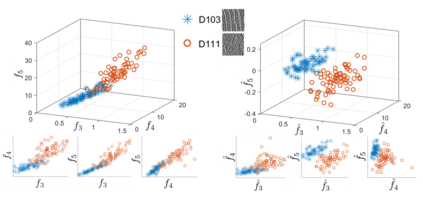
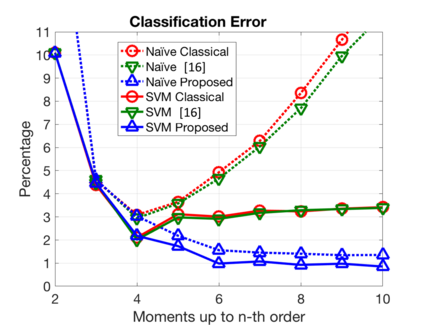
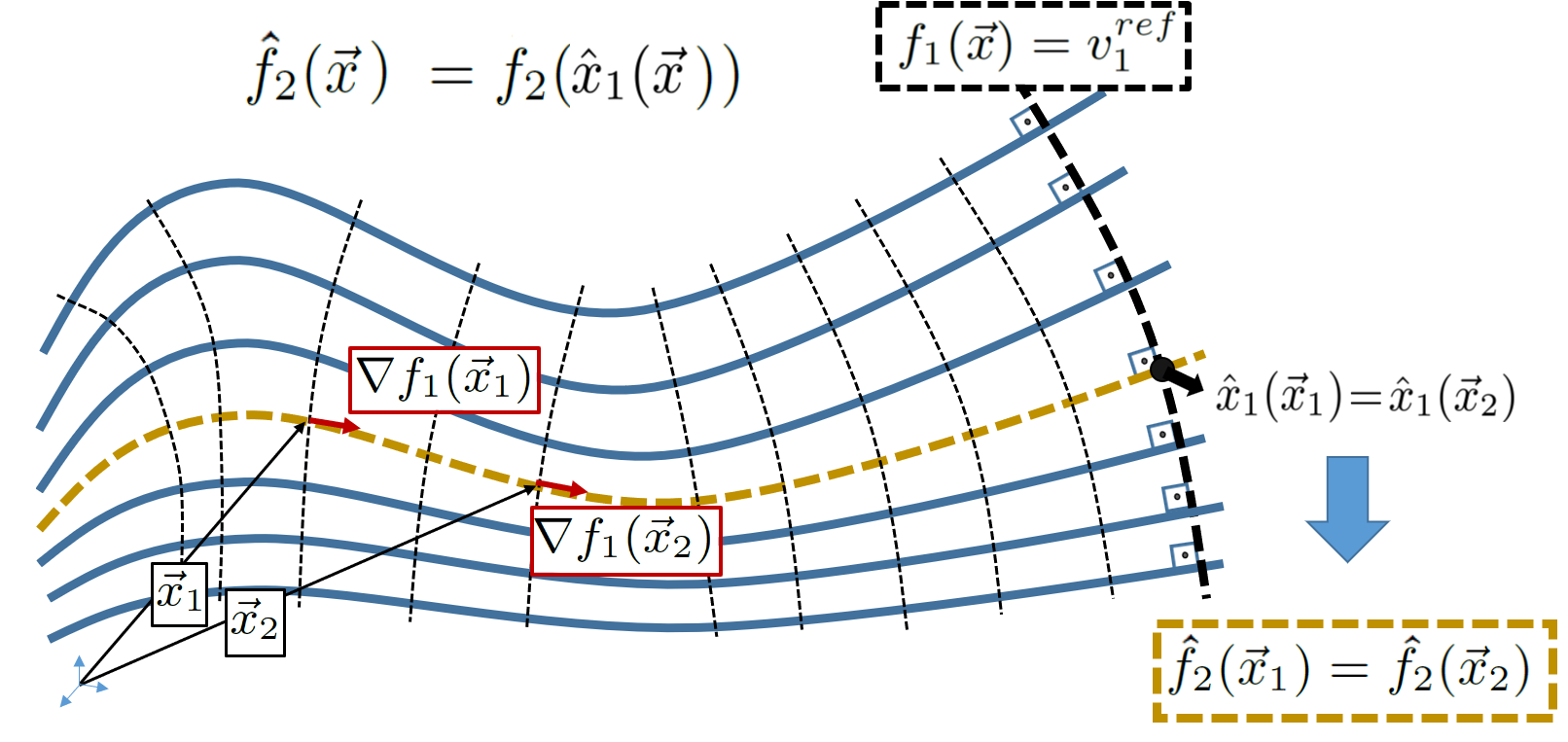
We introduce a method for deterministic decoupling of global features and show its applicability to improve data analysis performance, as well as to open new venues for feature transfer. We propose a new formalism that is based on defining transformations on submanifolds, by following trajectories along the features gradients. Through these transformations we define a normalization that, we demonstrate, allows for decoupling differentiable features. By applying this to sampling moments, we obtain a quasi-analytic solution for the orthokurtosis, a normalized version of the kurtosis that is not just decoupled from mean and variance, but also from skewness. We apply this method in the original data domain and at the output of a filter bank to regression and classification problems based on global descriptors, obtaining a consistent and significant improvement in performance as compared to using classical (non-decoupled) descriptors.
翻译:我们引入了一种确定性脱钩全球特征的方法,并展示了该方法可用于改进数据分析性能,以及打开特征转移的新场所。我们提出了一种新的形式主义,其依据是界定子层的变异,沿特征梯度沿轨运行。通过这些变异,我们定义了一种正常化,我们展示了这种变异性允许脱钩。通过将这一变异性特征应用到取样时刻,我们获得了一种半分析性溶液,一种对二次体分解的归正性,一种不仅与中值和差异脱钩,而且与偏差脱钩相分离的归正性版本。我们在原始数据领域和过滤库输出时采用了这种方法,以全球解码为根据的回归和分类问题,与使用古典(非分解的)脱钩器相比,在性能方面得到了一致和显著的改进。