Structure-preserving numerical method for Ampere-Nernst-Planck model

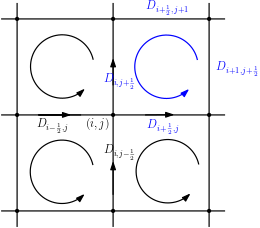
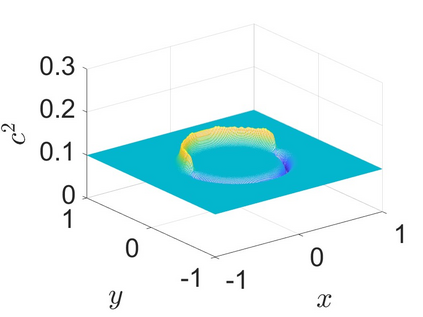
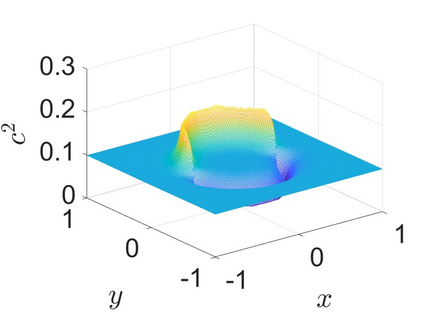
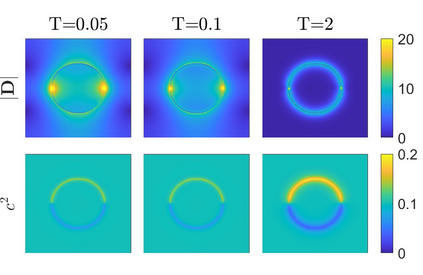
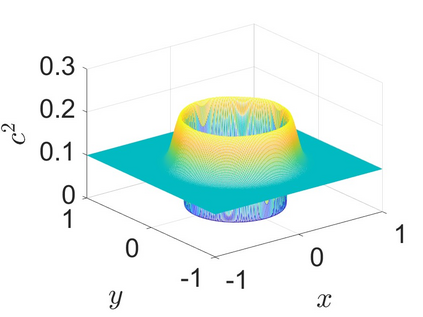
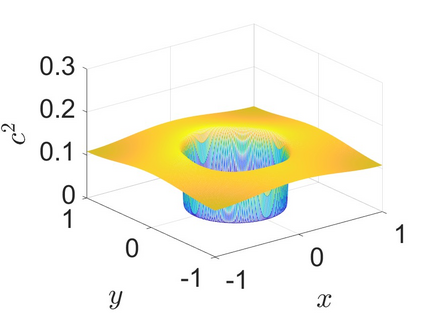
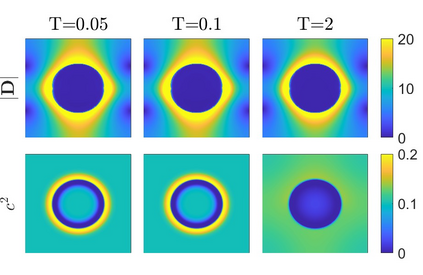
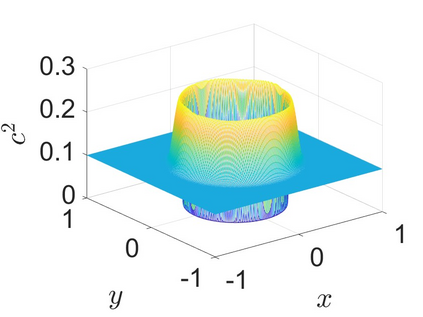
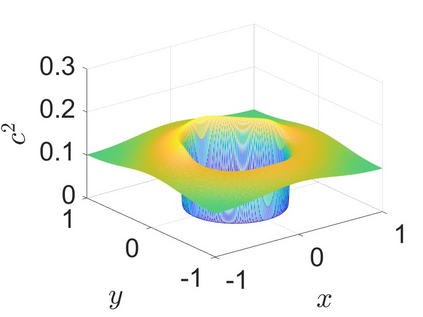
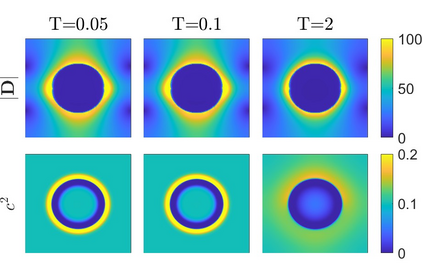
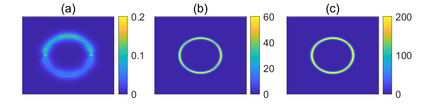
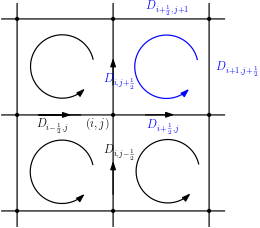
Charge dynamics play essential role in many practical applications such as semiconductors, electrochemical devices and transmembrane ion channels. An Amp\'{e}re-Nernst-Planck (ANP) model that describes charge dynamics via concentrations and the electric displacement is able to take effects beyond mean-field approximations into account. To obtain physically faithful numerical solutions, we develop a structure-preserving numerical method for the ANP model whose solution has several physical properties of importance. By the Slotboom transform with entropy-mean approximations, a positivity preserving scheme with Scharfetter-Gummel fluxes is derived for the generalized Nernst-Planck equations. To deal with the curl-free constraint, the dielectric displacement from the Amp\'{e}re equation is further updated with a local relaxation algorithm of linear computational complexity. We prove that the proposed numerical method unconditionally preserves the mass conservation and the solution positivity at the discrete level, and satisfies the discrete energy dissipation law with a mild time-step restriction. Numerical experiments verify that our numerical method has expected accuracy and structure-preserving properties. Applications to ion transport with large convection, arising from boundary-layer electric field and Born solvation interactions, further demonstrate that the ANP formulation with the proposed numerical scheme has attractive performance and can effectively describe charge dynamics with large convection of high numerical cell P\'{e}clet numbers.