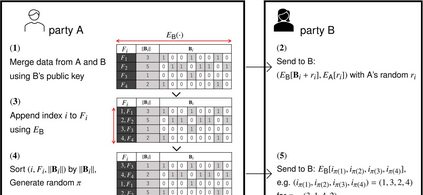
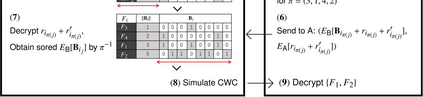
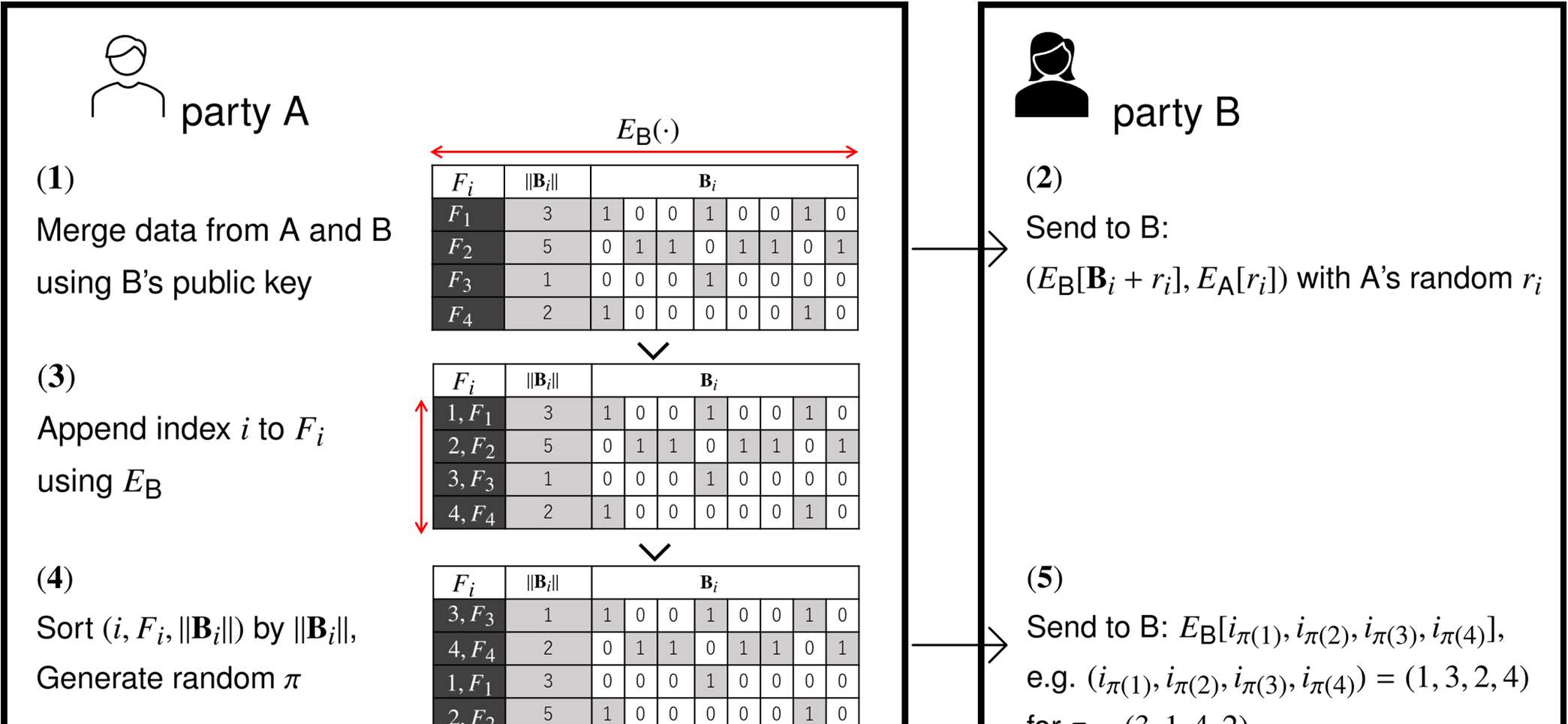
For the feature selection problem, we propose an efficient privacy-preserving algorithm. Let $D$, $F$, and $C$ be data, feature, and class sets, respectively, where the feature value $x(F_i)$ and the class label $x(C)$ are given for each $x\in D$ and $F_i \in F$. For a triple $(D,F,C)$, the feature selection problem is to find a consistent and minimal subset $F' \subseteq F$, where `consistent' means that, for any $x,y\in D$, $x(C)=y(C)$ if $x(F_i)=y(F_i)$ for $F_i\in F'$, and `minimal' means that any proper subset of $F'$ is no longer consistent. On distributed datasets, we consider feature selection as a privacy-preserving problem: Assume that semi-honest parties $\textsf A$ and $\textsf B$ have their own personal $D_{\textsf A}$ and $D_{\textsf B}$. The goal is to solve the feature selection problem for $D_{\textsf A}\cup D_{\textsf B}$ without revealing their privacy. In this paper, we propose a secure and efficient algorithm based on fully homomorphic encryption, and we implement our algorithm to show its effectiveness for various practical data. The proposed algorithm is the first one that can directly simulate the CWC (Combination of Weakest Components) algorithm on ciphertext, which is one of the best performers for the feature selection problem on the plaintext.
翻译:对于特性选择问题, 我们提出一个高效的隐私保存算法 。 设置选择问题在于找到一个一致和最小的子集$F\ subsetef F$, 其中“ 固定” 意指任何美元、 美元、 美元和 美元的数据、 特点和类组, 其中, 给每个美元( F_ i) 美元和类标签 $( C) 美元 美元 。 对于每美元( D, F, C) 和 美元 。 对于3 美元( D, F, F, C) 来说, 特性选择问题在于找到一个一致和最小的子子集 $F 。 如果“ 固定” 意指对于任何美元、 y\ 美元、 美元、 美元( C) y( C) y( C) 美元, 如果给美元( F) 美元) 和 美元( 美元) 类类的特性值值值值值值值, 则“ 最小 ” 表示任何正确的子选择都不再一致 。 在分发的数据集中, 我们觉得一个半字母缔约方 美元和 文本的半字母 美元 和 表示 美元, 和 美元 美元 自己选择的精精度 的精度 的精度 。