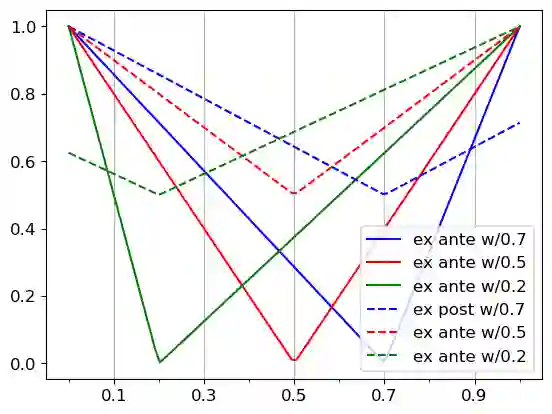
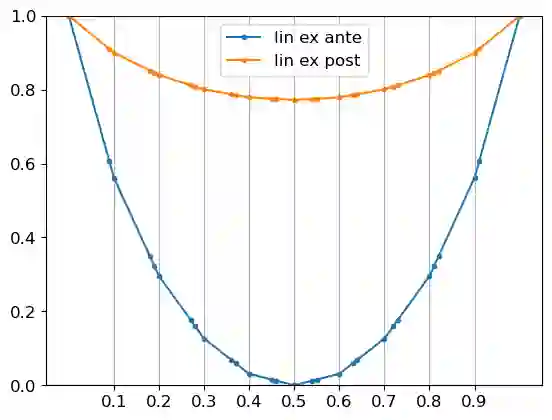
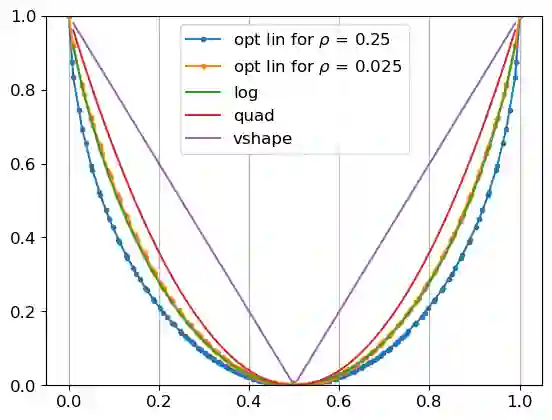
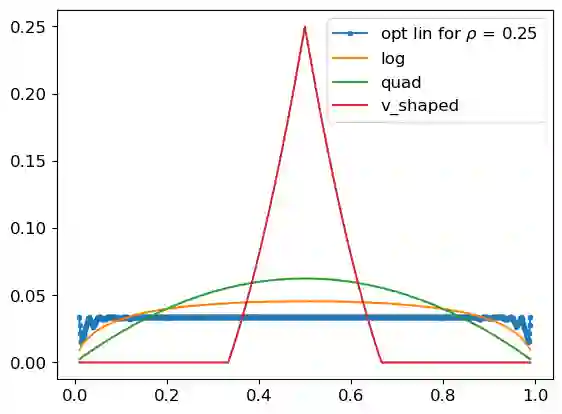
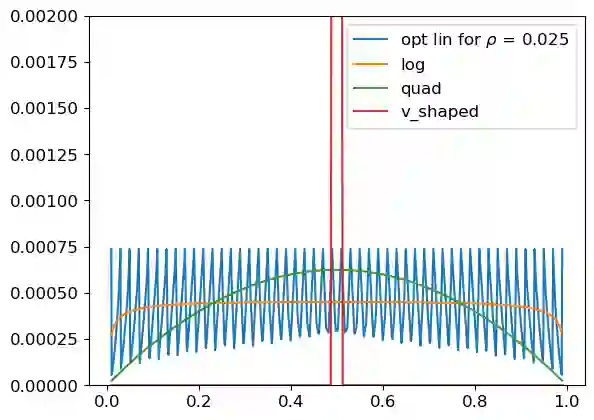
This paper studies the design of optimal proper scoring rules when the principal has partial knowledge of an agent's signal distribution. Recent work characterizes the proper scoring rules that maximize the increase of an agent's payoff when the agent chooses to access a costly signal to refine a posterior belief from her prior prediction, under the assumption that the agent's signal distribution is fully known to the principal. In our setting, the principal only knows about a set of distributions where the agent's signal distribution belongs. We formulate the scoring rule design problem as a max-min optimization that maximizes the worst-case increase in payoff across the set of distributions. We propose an efficient algorithm to compute an optimal scoring rule when the set of distributions is finite, and devise a fully polynomial-time approximation scheme that accommodates various infinite sets of distributions. We further remark that widely used scoring rules, such as the quadratic and log rules, as well as previously identified optimal scoring rules under full knowledge, can be far from optimal in our partial knowledge settings.
翻译:暂无翻译